Решение 1 страница

а. По определению градиента скалярного поля .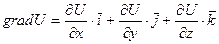

Находим частные производные функции :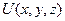

, ,

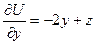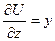
Таким образом .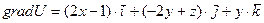

б. Аналогично пункту а), получим:

, ,

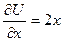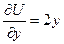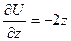
Таким образом .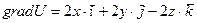

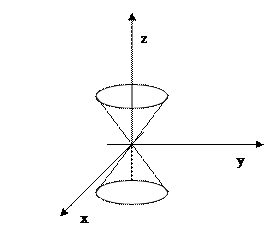
Построим поверхности уровня: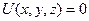

Тогда 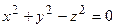, 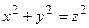‑ конус с вершиной в начале координат.

Если 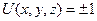, то :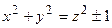

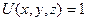
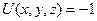
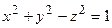
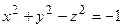
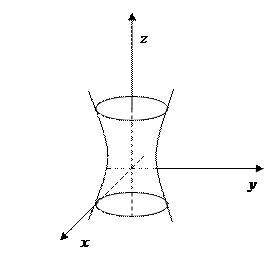
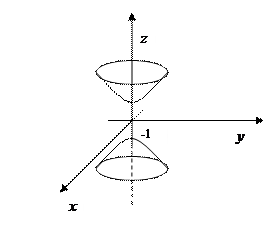
Однополостный Двуполостный

гиперболоид вращения гиперболоид вращения

вокруг оси 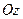вокруг оси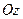

Пример 3: Найти векторные линии векторного поля :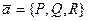

а.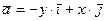

б.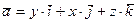

Решение:

а. Согласно определению, векторных линий:

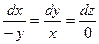, или .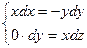

Решая систему, получаем . Таким образом, векторные линии данного поля представляют собой окружности с центрами на оси 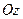, лежащие в плоскостях, перпендикулярных этой оси.

б. Аналогично предыдущему пункту, составляем систему

.

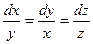Решим ее методом составления интегрируемых комбинаций:

Равенство 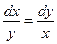образует первую интегрируемую комбинацию. Получаем 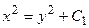. Для получения еще одной интегрируемой комбинации используем свойство пропорции: .

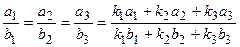Тогда, в нашем случае 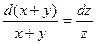. Интегрируя данное равенство, получаем .

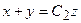Таким образом, векторные линии задаются системой:

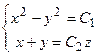
Т.е. векторные линии данного поля являются линиями пересечения гиперболических цилиндров 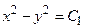с плоскостями .

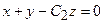Пример 4. Вычислить поток векторного поля 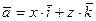через внешнюю сторону боковой поверхности цилиндра 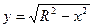, ограниченного плоскостями .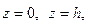

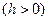Решение:

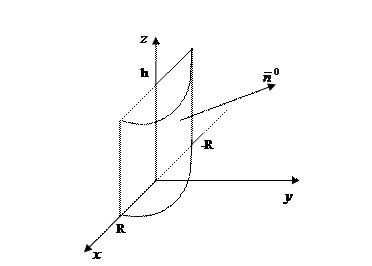
Вычислим поток векторного поля по формуле:

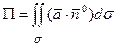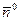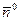, где ‑ нормальный единичный вектор к поверхности . Найдем вектор . Запишем уравнение поверхности в неявном виде: .

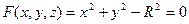Тогда 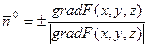. Т.к. 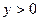(по условию задачи), то 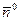образует острый угол с осью :

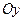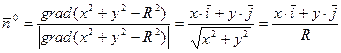
Следовательно, .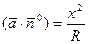

Поток векторного поля . Спроектируем поверхность : 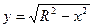на плоскость 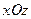, получим область 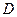, ограниченную линиями: .

=

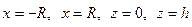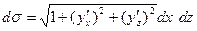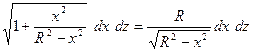
Таким образом,

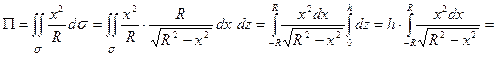(применяя подстановку 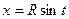, получаем) = .

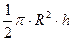Пример 5. Вычислить поток векторного поля

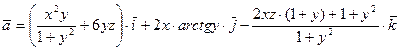
через внешнюю сторону части поверхности 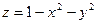, расположенной над плоскостью .

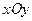Решение:

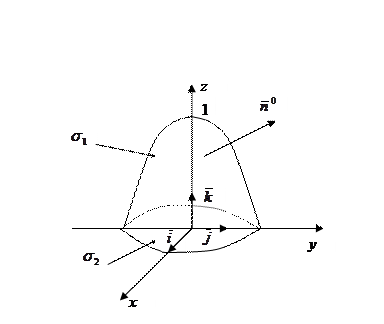
Замкнем данную поверхность куском плоскости 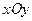, который ограничен окружностью 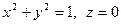. Тогда можем применить формулу Гаусса-Остроградского.

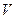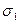Пусть ‑ объем полученного тела, ограниченного замкнутой кусочно-гладкой поверхностью , состоящей из части параболоида вращения 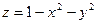и части 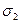плоскости .

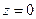Поток данного векторного поля через поверхность по теореме Гаусса-Остроградского равен:

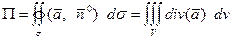
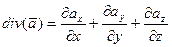, где .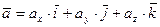

.

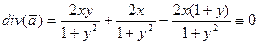Следовательно, поток

.

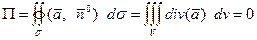В силу аддитивности потока будем иметь

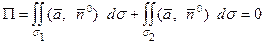
Отсюда искомый поток

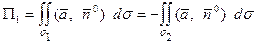
Найдем 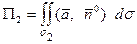. Так как на плоскости 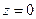, имеем

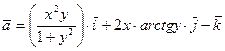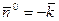, и тогда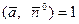

Таким образом, поток 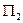через круг 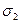будет равен площади круга : .

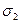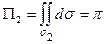Искомый поток .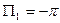

Пример 6. Вычислить работу векторного поля 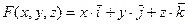вдоль линии 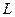, являющейся пересечением параболического цилиндра 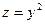с плоскостью 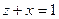от точки 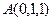до точки .

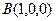Решение:

Зададим линию 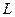параметрически: положив 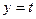, получим 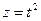, а 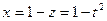. Тогда 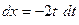, , 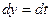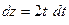. Точке 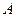соответствует значение параметра 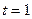, а точке 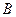‑ значение .

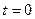Таким образом:

.

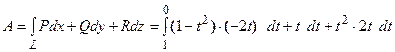
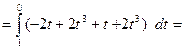
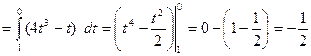Пример 7. Вычислить циркуляцию векторного поля

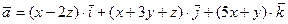
вдоль периметра треугольника с вершинами .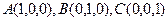

Решение:

По определению циркуляции 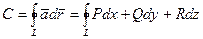, получаем

.

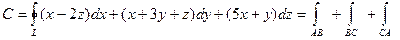На отрезке 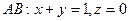, следовательно

.

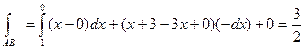На отрезке 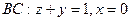, следовательно

.

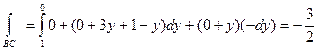На отрезке 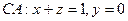, следовательно

.

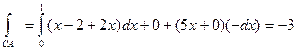Следовательно,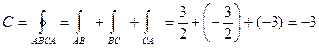

Пример 8. Найти циркуляцию вектора 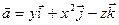по контуру 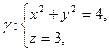непосредственно и по формуле Стокса.

Решение:

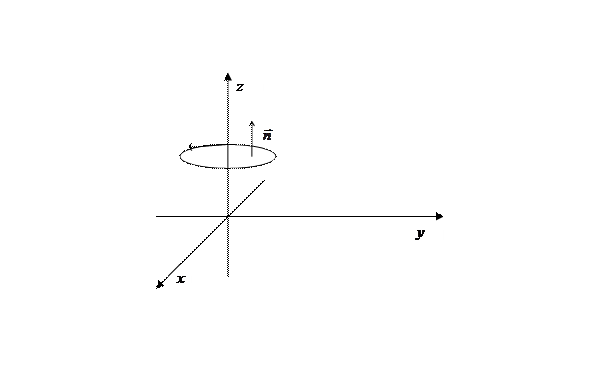
I способ.

Контур 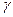- окружность радиуса 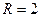, лежащая в плоскости 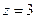. Выберем ориентацию как показано на рисунке, т.е. против часовой стрелки. Параметрические уравнения окружности имеют вид 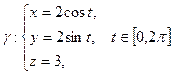, так что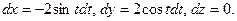

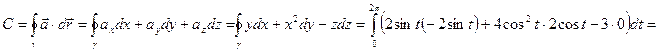
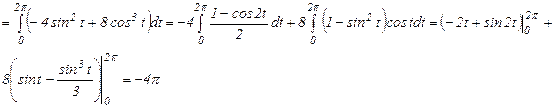
II способ.

Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность 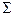, натянутую на контур 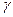. Естественно в качестве 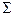взять круг, имеющий контур 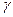своей границей. Уравнение поверхности 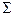имеет вид: 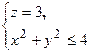. Согласно выбранной ориентации контура нормаль к поверхности необходимо взять равной .

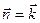Далее .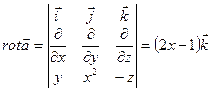

В силу теоремы Стокса

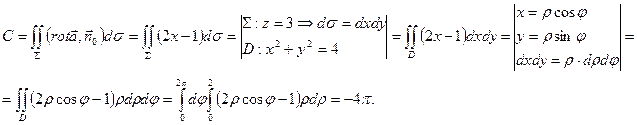
Пример 9. Доказать, что векторное поле 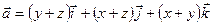является потенциальным. Найти его потенциал.

Решение:

Необходимым и достаточным условием потенциальности поля является равенство нулю вихря поля. В нашем случае

.

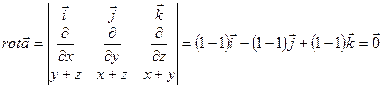Таким образом, поле является потенциальным.

Обозначим 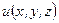- искомый потенциал. По определению потенциального поля, поле градиента искомой функции 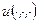должно совпадать с векторным полем 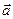. Поэтому

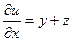. Отсюда 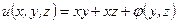, где 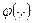- некоторая функция аргументов 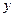и 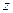. Из условия , можно сделать вывод, что 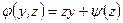. Таким образом, 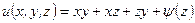. Неопределенную функцию 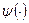найдем из условия 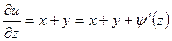. Решением последнего уравнения является функция .

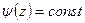В итоге потенциал имеет вид .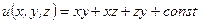

Пример 10. Пусть 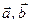- произвольные векторные поля. Показать, что 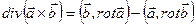(символом 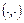обозначено скалярное произведение векторов).

Решение:

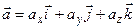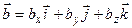Пусть и - произвольные векторные поля. Найдем векторное произведение .

.

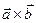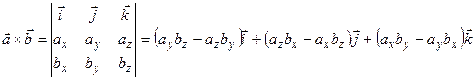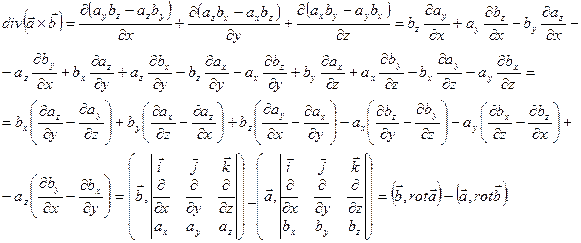
Вариант 1.

Задание 1. Найти производную скалярного поля 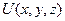в точке 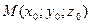по направлению нормали к поверхности , образующей острый угол с положительным направлением оси :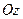

,

, .

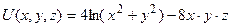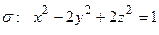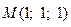Задание 2. Найти градиент скалярного поля 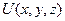и построить поверхности уровня для заданных значений :

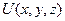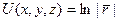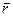, где ‑ радиус-вектор точки поля, .

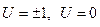Задание 3. Найти векторные линии векторного поля :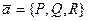

.

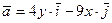Задание 4. Найти поток векторного поля 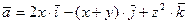через

а)полную поверхность цилиндра ;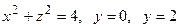

б) основание этого цилиндра, лежащее в плоскости 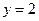в положительном направлении оси .

Задание 5. Найти поток векторного поля 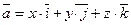через плоскость 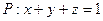, расположенную в первом октанте (нормаль образует острый угол с осью Oz).

Задание 6. Вычислить поток векторного поля 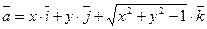через внешнюю сторону однополостного гиперболоида 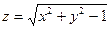, ограниченного плоскостями .

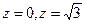Задание 7. Найти работу силы 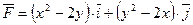, при перемещении материальной точки вдоль линии 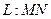от точки 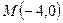до точки .

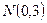Задание 8. Найти циркуляцию векторного поля 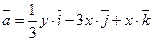вдоль контура 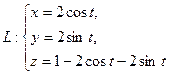в направлении, соответствующем возрастанию параметра .

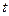Задание 9. Найти циркуляцию векторного поля 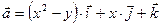по контуру 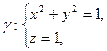непосредственно и по формуле Стокса.

Задание 10. Показать потенциальность векторного поля 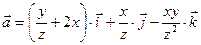. Найти его потенциал.

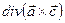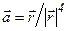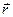Задание 11. Найти , где , - радиус-вектор точки поля, 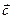‑ постоянный вектор.

Вариант 2.

Задание 1. Найти производную скалярного поля 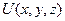в точке 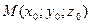по направлению нормали к поверхности , образующей острый угол с положительным направлением оси :

,

, .

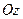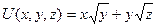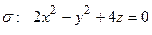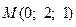Задание 2. Найти градиент скалярного поля 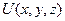и построить поверхности уровня для заданных значений :

, .

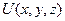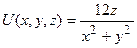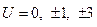Задание 3. Найти векторные линии векторного поля :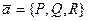

.

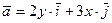Задание 4. Найти поток векторного поля 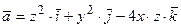через

а) полную поверхность призмы, ограниченной плоскостями ;

б) верхнее основание этой призмы в положительном направлении оси .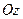

Задание 5. Найти поток векторного поля 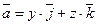через плоскость 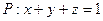, расположенную в первом октанте (нормаль образует острый угол с осью Oz).

Задание 6. Вычислить поток векторного поля через внешнюю сторону параболоида 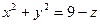, расположенного в первом октанте.

Задание 7. Найти работу силы 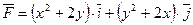, при перемещении материальной точки вдоль линии 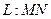от точки 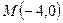до точки .

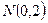Задание 8. Найти циркуляцию векторного поля 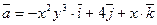вдоль контура 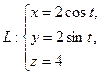в направлении, соответствующем возрастанию параметра .

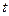Задание 9. Найти циркуляцию векторного поля 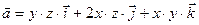по контуру 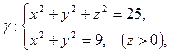непосредственно и по формуле Стокса.

Задание 10. Показать потенциальность векторного поля 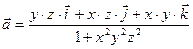. Найти его потенциал.

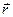Задание 11. Доказать, что векторное поле , где ‑ радиус-вектор точки поля, будет соленоидальным, если .

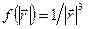Вариант 3.

Задание 1. Найти производную скалярного поля 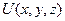в точке 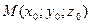по направлению нормали к поверхности , образующей острый угол с положительным направлением оси :

,

, .

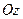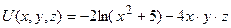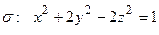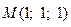Задание 2. Найти градиент скалярного поля 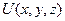и построить поверхности уровня для заданных значений :

, .

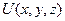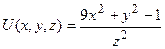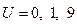Задание 3. Найти векторные линии векторного поля :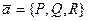

.

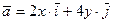Задание 4. Найти поток векторного поля 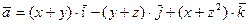через

а) полную поверхность пирамиды, вершины которой ;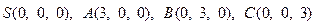

б) грань 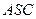в положительном направлении оси .

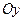Задание 5. Найти поток векторного поля 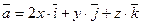через плоскость 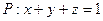, расположенную в первом октанте (нормаль образует острый угол с осью Oz).

Задание 6. Найти поток векторного поля 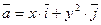через часть поверхности 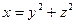, отсеченной плоскостью 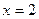в направлении внешней нормали.

Дата добавления: 2014-10-31