Нормальное распределение. Нормальный закон распределения – самый распространенный в природе

Нормальный закон распределения – самый распространенный в природе. Он описывает явления, на которые влияет большое число незначительных факторов. Особое значение этот закон имеет в технике и, в частности, в строительстве. Большое число самых разных технических характеристик, имеющих разброс значений вследствие неоднородности химического состава и физических свойств материалов, невозможности полного совпадения параметров повторяющихся технологических операций, ненулевых допусков изделий и конструкций, неточностей и субъективности измерений и т.п., подчиняются нормальному закону.

Плотность нормального распределения вероятностей непрерывной случайной величины описывается формулой:

, (3.17)

где a - математическое ожидание;

- среднеквадратическое отклонение (стандарт).

Эта функция симметрична относительно ее математического ожидания (рис. 3.1, а).

Функция распределения нормального закона имеет вид (рис. 3.1, б):

, (3.18)

	а
	б

Рис. 3.1. Плотность и функция распределения нормального закона

При a=0 и формулы (3.17) и (3.18) принимают вид:

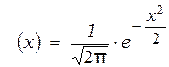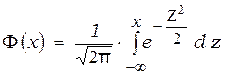; . (3.19)

Эти функции называются нормированными и являются табличными.

От реального распределения к нормированному можно перейти, введя новую переменную , которая по существу обозначает, на каком расстоянии (выраженном в количестве стандартов) от математического ожидания находится текущее значение случайной величины x.

Наличие нормированных табличных функций помогает решить следующие прикладные задачи:

1) Найти вероятность попадания нормальной случайной величины в заданный интервал :

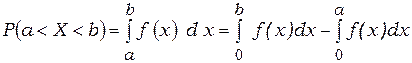; (3.20)

Пример.

Значения предела текучести стали 15ХСНД распределены по нормальному закону. Среднее значение равно 360 МПа, стандарт распределения – 11 МПа.

Найти вероятность того, что при испытании образца предел текучести окажется в пределах (340 – 350) МПа.

Введем переменную . По формуле (3.20) имеем:

.

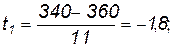
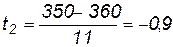Р (340 < x < 350) = P (-1,8 < t < 0,9) = Ф(-0,9) – Ф(-1,8) = Ф(1,8) – Ф(0,9).

Из таблицы Ф(1,8) = 0,4641; Ф(0,9) = 0,3159.

Искомая вероятность равна 0,1482.

2) Найти вероятность заданного отклонения d случайной величины от ее математического ожидания т.е. :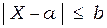

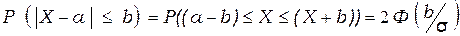. (3.21)

Пример.

В условиях предыдущего примера найти вероятность того, что отклонение предела текучести от среднего значения будет находиться в пределах .

Отношение . Из таблицы Ф(0,45) = 0,1736.

По формуле (3.21) искомая вероятность равна:

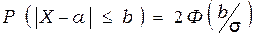= 2 х 0,1736 = 0,3472.

Распределение суммы независимых случайных величин

Z = X + Y.

Плотность распределения суммы независимых случайных величин определяется по формуле:

, (3.22)

Плотность распределения суммы независимых случайных величин называют композицией.

Нормальный закон обладает свойством устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, в котором

M(Z)=M(X)+M(У);

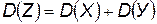. (3.23)

Контрольные вопросы

1. Перечислите законы распределения вероятностей.

2. Укажите связь между биноминальным распределением и распределением Пуассона.

3. Что такое показательный закон надежности?

4. Объясните природу нормального распределения.

5. Что такое нормированное нормальное распределение?

Дата добавления: 2014-10-31