Виды выборок

Понятия математической статистики

Проверка правдоподобия гипотез

Определение закона распределения случайной величины по статистическим данным

Основные задачи математической статистики

Элементы математической статистики

Стационарные и марковские случайные процессы

Случайные процессы, математические ожидания и дисперсии которых постоянны во времени, называются стационарными.

Примером стационарного процесса могут служить колебания пролетного строения при установившемся режиме автомобильного движения.

В случае стационарного процесса корреляционная функция зависит только от промежутка между первым и вторым значениями аргумента.

K_x (t_{1 ,} t +t) = K_x (t). (4.2)

Марковским называется случайный процесс X(t), если для каждого момента времени t₀ протекание случайного процесса в будущем (при t > t₀) определяется его настоящим (значение X (t₀)) и не зависит от прошлого (от значений X(t) при t < t₀).

Пример.

Р азвитие силовой трещины в железобетоне в каждый момент времени определяется ее шириной, длиной, конфигурацией и не зависит от того, как это состояние образовалось.

Математическая статистика – наука о методах регистрации, описании и анализе статистических экспериментальных данных, полученных в результате наблюдения многократно повторяющихся случайных явлений.

Закономерности, наблюдаемые в многократно повторяющихся явлениях, проявляются тем больше, чем больше статистических данных об этих явлениях.

На практике приходится иметь дело с ограниченным количеством экспериментальных данных. Методика обработки этих данных должна обеспечивать выявление типичных характеристик изучаемых случайных явлений, законов распределения случайных величин, отражающих эти явления количественно.

Анализ статистических данных должен подтвердить или опровергнуть выдвинутую заранее гипотезу о законе распределения изучаемой случайной величины, или о некоторой зависимости между двумя случайными величинами.

Генеральной совокупностью называют всю совокупность изучаемых объектов.

Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов.

Повторной выборкой или выборкой с возвратом называют выборку, когда объект возвращается в генеральную совокупность.

Бесповторной называют выборку, когда объект в генеральную совокупность не возвращается.

Пример. Средний по стране коэффициент вариации прочности бетона, составляющий n = 13,5%, получен по генеральной совокупности, обобщающей данные по всем заводам ЖБК.

Коэффициент вариации прочности конкретной партии бетона определяют на выборке образцов, объем которой обычно регламентирован нормами.

5.2.2. Частота. Полигон и гистограмма

Значения х_i случайной величины X, полученные в выборке объемом n, расположенные в возрастающем или убывающем порядке, составляют вариационный ряд.

Количество появлений n_i в выборке каждого значения х_i называют его частотой, а отношение 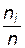– относительной частотой.

Очевидно, что S n_i = n, а S.

Массив измеренных значений случайной величины часто бывает удобней представить в виде графика. Для дискретных величин целесообразно строить так называемый полигон частот.

Полигоном частот называют ломаную, отрезки которой соединяют точки (x_i, n_i), i =1, 2,..., k,

где x_i – i -ое значение, откладывается на оси абсцисс;

n_i – количество появлений i-ого значения, откладывается на оси ординат;

k – число различных измеренных значений случайной величины.

В полигоне относительных частот последние откладываются на оси ординат и представляют собой отношение .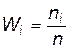

Параметры строительных конструкций и материалов являются, как правило, непрерывными случайными величинами. В этом случае лучше использовать графики частот в виде гистограмм.

Гистограмма частот – ступенчатый график по интервалам h (ось абсцисс) с соответствующими плотностями абсолютных или относительных 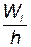частот.

Приведем для примера гистограмму относительных частот выборки результатов измерения прочности бетона (рис. 5.1).

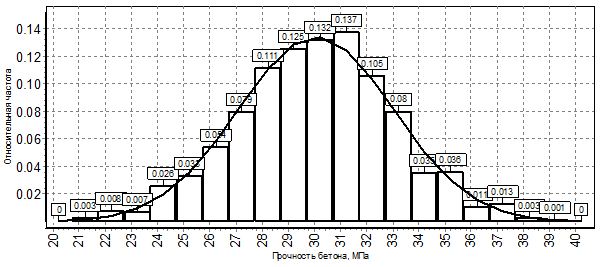
Рис. 5.1. Гистограмма измерений прочности бетона

Дата добавления: 2014-10-31