Относительная частота. Статистическое определение вероятности

Классическое определение вероятности

Для практической деятельности важно уметь сравнивать события по степени возможности их поступления. Очевидно, события: «выпадение дождя» и «выпадение снега» в первый день лета в данной местности, «выигрыш по одному билету» и «выигрыш по одному из n приобретённых билетов» денежно-вещевой лотереи – обладают разной степенью возможности их наступления. Поэтому для сравнения событий нужна определённая мера.

Опр. Численная мера степени объективной возможности наступления события называется вероятностью события.

Это определение, качественно отражающее понятие вероятности события, не является математическим. Чтобы оно таким стало, необходимо определить его количественно.

Опр. События, образующие полную группу, т.е. события единственно возможные, несовместные и равновозможные, будем называть элементарными событиями (исходами, случаями, шансами).

Опр. Событие называется благоприятствующим (благоприятным) событию В, если появление события А влечёт за собой появление события В.

Опр. (Классическое определение вероятности).

Вероятность события равна отношению числа случаев (исходов), благоприятствующих ему, к общему числу случаев (исходов), т.е.

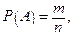(1)

где

Р(А) – вероятность события А;

m – число случаев (исходов), благоприятствующих событию А;

n – общее число случаев (исходов).

Классическое определение (точнее, классическая формула) вероятности (1) долгое время, с XVII вплоть до XIX вв., рассматривалась действительно как определение вероятности, так как в то время методы теории вероятностей применялись в основном к азартным играм, которые сводились к схеме случаев, или в задачах, которые искусственно сводились к этой схеме. В настоящее время формальное определение вероятности не даётся (это понятие считается первичным и не определяется), а при его пояснении используют понятие относительной частоты события (см. ниже 1.3).

Поэтому, классическое определение (классическую формулу) вероятности следует рассматривать не как определение, а как метод вычисления вероятностей для испытаний, сводящихся к схеме случаев.

Свойства вероятности события:

1 Вероятность любого события есть положительное число, заключённое между нулём и единицей, т.е.

0 ≤ Р(А) ≤ 1.

2 Вероятность достоверного события равна единице.

3 Вероятность невозможного события равна нулю.

События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными событиями.

Пример 1. Вычислите вероятность выпадения герба при одном бросании монеты.

Решение

Очевидно, событие – «выпадение герба» и событие – «выпадение решки» – образуют полную группу событий несовместных и равновозможных, т.е. . Событию благоприятствует лишь одно событие – само , здесь 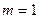. Поэтому

Ответ: 0,5.

Пример 2. При бросании игральной костивозможны шесть исходов – выпадение 1, 2, 3, 4, 5, 6 очков. Какова вероятность появления чётного числа очков?

Решение

Все 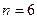исходов образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Событию – «появление чётного числа очков» благоприятствуют 3 исхода (случая) – 2, 4, 6 очков. Тогда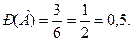

Ответ: 0,5. [4, с.18-20]

Ранее было отмечено, что классическое определение вероятности применимо только для тех событий, которые могут появиться в результате испытаний, обладающих симметрией возможных исходов, т.е. сводящихся к схеме случаев. Но существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения. В первую очередь это события, которые не являются равновозможными исходами испытаний. Например, при бросании неправильной игральной кости выпадение различных граней не является равновозможным. Или, если монета сплющена, то, очевидно, что события «появление герба» и «появление решки» нельзя считать равновозможными. Таким образом, формула (1) для расчёта вероятности любого из них окажется неприемлема.

В таких случаях используется статистическое определение вероятности.

Опр. Статистической вероятностью события называется относительная частота (частость) появления этого события в n произведённых испытаниях, то есть,

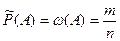, (2)

где

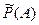- статистическая вероятность события ;

- относительная частота (частость) события ;

m – число испытаний, в которых появилось событие ;

n – общее число испытаний.

В отличие от «математической» вероятности 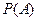, рассматриваемой в классическом определении, статистическая вероятность 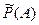является характеристикой опытной, экспериментальной. Если 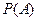есть доля случаев, благоприятствующих событию , которая определяется непосредственно, без каких-либо испытаний, то 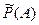есть доля тех фактически произведённых испытаний, в которых событие появилось.

Статистическое определение вероятности, как и понятия и методы теории вероятностей в целом, применимы не к любым событиям с неопределённым исходом, которые в житейской практике считаются случайными, а только к тем из них, которые обладают определёнными свойствами.

1. Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.

2. События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот, т.е. в различных сериях испытаний относительная частота (частость) события изменяется незначительно (тем меньше, чем больше число испытаний), колеблясь около постоянного числа. Причём, этим постоянным числом является вероятность события.

Факт приближения относительной частоты, или частости события к его вероятности при увеличении числа испытаний, сводящихся к схеме случаев, подтверждается многочисленными массовыми экспериментами.

3. Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, т.к. только в этом случае можно считать вероятность события 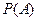приближённо равной её относительной частоте.

Пример 3. Было проведено 10 серий бросания монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484. Все эти частоты группируются около числа 0,5.

Рассмотрим ещё один пример с бросанием монеты.

Пример 4. Данные результатов бросания монеты приведены в таблице 1.

Таблица 1. Результаты выпадения герба при бросании монеты.

Экспериментатор	Число бросаний	Число выпадений герба	Относительная частота
Бюффон	4 040	2 048	0,5069
К. Пирсон	12 000	6 019	0,5016
К. Пирсон	24 000	12 012	0,5005

Здесь относительные частоты незначительно отклоняются от числа 0,5, причём тем меньше, чем больше испытаний. При 4 040 испытаниях отклонение равно 0,0069, а при 24 000 – 0,0005.

Дата добавления: 2014-10-31