Формула Пуассона

Схема Бернулли

В приложениях теории вероятностей часто встречается некоторая стандартная схема, называемая схемой независимых испытаний или схемой Бернулли. Имеет место теорема.

Теорема. Если вероятность 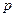наступления событии А в каждом испытании постоянна, то вероятность того, что событие А наступит т раз в 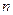независимых испытания, равна

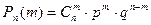, (19)

или

(19*)

где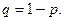

Вероятность того, что событие наступит: а) менее 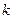раз; б) более 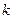раз; в) не менее 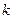раз; г) не более 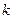раз – находят соответственно по формулам:

а)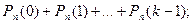

б)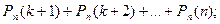

в)

г) 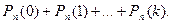(20)

Опр. Число 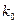, которому при заданном 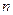соответствует максимальная биномиальная вероятность 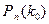, называется наивероятнейшим.

Для нахождения наивероятнейшего числа 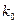по заданным 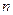и р можно воспользоваться неравенствами

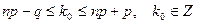, (21)

причем:

а) если число 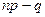- дробное, то существует одно наивероятнейшее число ;

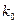б) если число 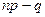- целое, то существует два наивероятнейших числа: 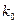и ;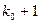

в) если число 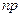- целое, то наивероятнейшее число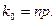

*Пусть производится 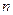независимых опытов, каждый из которых имеет т 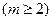попарно несовместных и единственно возможных сходов 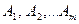с вероятностями 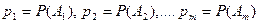, одинаковыми во всех опытах (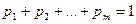). Для произвольных целых неотрицательных чисел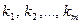 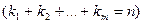обозначим через 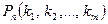вероятность того, что в 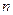опытах исход 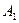наступит 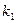раз, исход 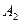наступит 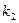раз и т.д., исход 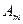наступит 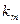раз. Тогда справедлива формула

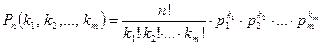, (22)

которая является обобщением формулы Бернулли на случай, когда каждый из независимых опытов 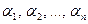имеет т исходов .

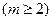Пример 10. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?

Решение.

Так как играют равносильные шахматисты, то вероятность выигрыша 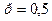, следовательно, вероятность проигрыша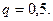

Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.

Найдем вероятность того, что две партии из четырех будут выиграны. Воспользуемся формулой 19*:

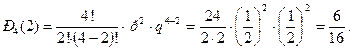
Найдем вероятность того, что три партии из шести будут выиграны:

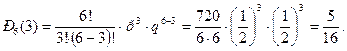
Так как 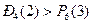, то вероятнее выиграть две партии из четырех, чем три из шести.

Ответ: вероятнее выиграть две партии из четырех. [2, с.46-47]

Пример 11. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найдите наивероятнейшее число образцов, которые товаровед признает годными к продаже.

Решение.

По условию 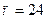, , 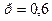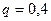. Воспользуемся неравенством 21:

.

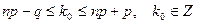Подставляя данные задачи, получим

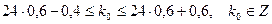
или

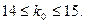
Так как - целое число, то наивероятнейших чисел два: 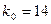и .

Ответ: 14; 15. [2, с.58-59]

Но в жизни встречаются задачи, когда 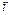и 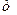- велики, а 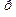- мало. Например, 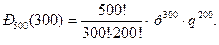Ясно, что в этом случае воспользоваться формулой Бернулли технически очень сложно. Возникает необходимость в желании иметь более простые приближенные формулы для вычисления вероятности при больших . Такие формулы, называемые асимптотическими, существуют и определяются теоремой Пуассона, локальной и интегральной теоремами Муавра-Лапласа. Наиболее простоя из них является теорема Пуассона.

При больших и малых 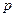имеет место теорема.

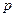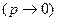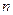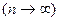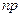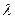
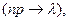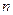Теорема. Если вероятность наступления события в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний , причем произведение стремиться к постоянному числу то вероятность того, что событие появится т раз в независимых испытаниях, удовлетворяет предельному равенству

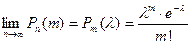
Итак, если вероятность 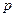– постоянна и мала, число испытаний 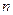– велико и число 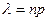- незначительно (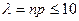). То из предельного равенства вытекает приближенная формула Пуассона:

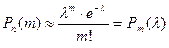(23)

Функция Пуассона 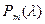табулирована (см. таблице 3 приложений [4, с.556]), но можно воспользоваться и значениями:

….

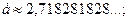
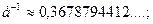
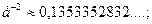
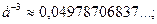
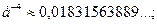
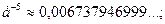
Пример 12. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?

Решение.

Из условия задачи следует, что , , .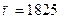

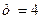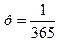Найдем 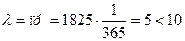, т. е. условие 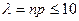- выполняется, можно воспользоваться формулой 23 и таблицей 3 «Значения функции Пуассона»:

.

Ответ: 0,1755. [4, с.72-73]

Дата добавления: 2014-10-31