Локальная и интегральная теоремы Муавра - Лапласа

Имеет место теорема.

Теорема. (Локальная теорема Муавра-Лапласа)

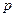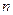Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, то вероятностьтого, что событие произойдет т раз в независимых испытаниях при достаточно большом числе 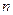, приближенно равна

, (24)

где

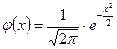- функция Гаусса (25)

и

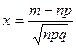. (26)

Чем больше 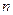, тем точнее приближенная формула (24). Как правило, на практике используется при условии 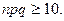Функция 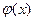табулирована, ее значения приведены в таблице 1 приложения [4, с.553-554].

Пользуясь данной таблицей, необходимо использовать свойства функции .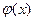

1. Функция 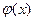является четной, т.е. .

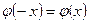2. Функция 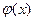- монотонно убывающая при положительных значениях х, причем, при .

Считают, что при .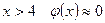

Теорема. (Интегральная теорема Муавра-Лапласа)

Если вероятность 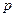наступления события в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число т наступления события в 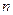независимых испытаниях заключено в пределах от до 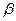(включительно), при достаточно большом числе 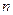, приближенно равна

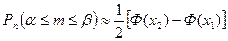, (27)

где

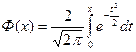- функция Лапласа, (28)

и

. (29)

Чем больше 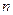, тем точнее приближенная формула (27). Как правило, на практике используется при условии Функция табулирована, ее значения приведены в таблице 2 приложения [4, с.555]. Пользуясь данной таблицей, необходимо использовать свойства функции

1. Функция является нечетной, т.е.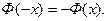

2. Функция - монотонно возрастающая при положительных значениях х, причем, при .

Считают, что при .

Замечание. Приближенными формулами Муавра – Лапласа 24 и 27 пользуются в случае, при Если же 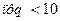, то эти формулы приводят к довольно большим погрешностям.

Рассмотрим следствие интегральной теоремы Муавра-Лапласа.

Следствие. Если вероятность 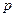наступления события в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе 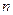независимых испытаний вероятность того, что:

а) число т наступлений события отличается от произведения 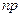не более, чем на величину (по абсолютной величине), т.е.

; (30)

б) частость события заключена в пределах от до 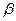(включительно), т.е.

, (31)

где

;(32)

в) частость события отличается от его вероятности 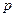не более, чем на величину (по абсолютной величине), т.е.

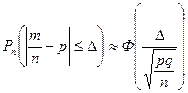. (33) [4, с.73-77]

Пример 13. Вероятность наступления события А в каждом из 900 независимых испытаний равна . Найдите вероятность того, что событие А произойдет: а) 710 раз; б) от 710 до 740 раз.

Решение.

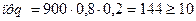а) Дано: , , , . Так как , то воспользовавшись формулами 24-26, четностью функции 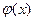и таблицей 1 приложения [4, с.553-554], получаем:

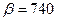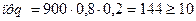б) Дано: , , , , . Так как , то воспользовавшись формулами 27-29, нечетностью функции и таблицей 2 приложения [4, с.555], получаем:

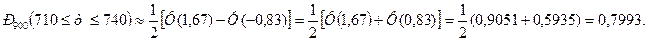Ответ: а) 0,0236; б) 0,7993.

Список используемой литературы:

1. Андрухаев, Хазерталь Махмудович. Сборник задач по теории вероятностей [Текст]: учебное пособие для студентов пед. ин-тов по спец. 2104 «Математика», «Математика с доп. спец. Физика» и 2105 «Физика с доп. спец. математика»/ Под ред. А.С. Солодовникова. –М.: Просвещение, 1985. -160 с.

2. Гмурман, Владимир Ефимович. Руководство к решению задач по теории вероятностей и математической статистике [Текст]: учебное пособие для втузов / В. Е. Гмурман. - 2-е изд., перераб. и доп. - М.: Высшая школа, 1975. - 333 с.

3. Карасев, Анатолий Иванович. Теория вероятностей и математическая статистика [Текст]: учебник для экономических специальностей вузов/ А.И. Карасев. Изд. 3-е, перераб. И доп. М., «Статистика», 177. -279 с.

4. Кремер, Наум Шевелевич. Теория вероятностей и математическая статистика [Текст]: учебник для вузов / Н. Ш. Кремер. - 2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2006. - 573 с.

Дата добавления: 2014-10-31