Точность оценки. Доверительная вероятность и доверительный интервал

Критерий согласия Пирсона (вторая задача математической статистики)

Подбор теоретического закона распределения (первая задача математической статистики).

Числовые характеристики статистического распределения

Эти характеристики - аналоги вероятностных параметров случайных величин.

Статистическое среднее выборки определяется по формуле, аналогичной выражению для математического ожидания случайной величины:

m _x = 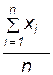(5.1)

Статистическая оценка дисперсии выборки по отношению к аналогичной вероятностной формуле берется с поправкой (обоснование этого коэффициента приводится в курсах теории вероятностей). Таким образом,

D(X) = (5.2)

Как правило, принципиальный вид теоретической кривой выбирается заранее, исходя из природы случайной величины. В некоторых случаях теоретическое распределение подбирается по внешнему виду статистического распределения.

При этом параметры теоретического распределения подбираются по методу моментов.

Начальным моментом s -го порядка дискретной случайной величины называется сумма вида

а _s(x) = , (5.3)

где x_i – значения случайной величины;

p_i – вероятности значений x_i;

n – число различных значений x_i.

Центральным моментом s -го порядка называют выражение

M_s = 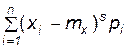, (5.4)

где m_x – математическое ожидание (среднее статистическое) случайной величины.

Очевидно, начальным моментом 1-го порядка является математическое ожидание (среднее статистическое):

a ₁(x) = m_x = . (5.5)

Центральный момент второго порядка – дисперсия

М₂ (x) = D_x = 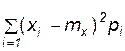. (5.6)

Смысл метода моментов заключается в следующем:

- моменты теоретического распределения приравниваются к моментам статистического распределения;

- число приравниваемых моментов должно равняться числу параметров теоретического распределения, для нормального распределения это число равно двум,

- практика показывает, что не следует рассматривать более четырех моментов.

Критерии согласия служат для оценки правильности аппроксимации данного статистического распределения теоретической кривой.

Пусть имеется статистическое распределение n значений случайной величины F^*(X) и имеется гипотеза H, состоящая в том, что величина x имеет функцию распределения F(x).

Для того, чтобы принять или опровергнуть гипотезу H, рассмотрим некоторую величину (χ²), характеризующую меру расхождения теоретического и статистического распределений. Эта величина определяется следующим образом.

Представим статистическое распределение случайной величины F^*(X) в виде гистограммы с интервалом h и подсчитаем частоты попадания значения n_i функции F^*(X) в каждый интервал. Определим также вероятности p_i попадания в соответствующие интервалы теоретической функции F (x).

Мера расхождения χ² вычисляется по формуле:

χ²=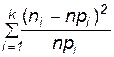=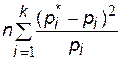, (5.7)

здесь с_i – «вес» интервала, который берется равным с_i = ;

k – число интервалов;

p_i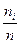^*= - относительная частота попадания в i -й интервал значений функции F^*(X).

Очевидно, что мера χ² также является случайной величиной, зависящей от теоретического закона F (x) и числа опытов n.

Меру χ² , вычисленную по формуле (5.7), сопоставляют с критическим значением χ²_кр , выбираемым по специальным таблицам в зависимости от надежности Р, с которой мы проверяем принятую гипотезу, а также от n – числа значений случайной величины F ^*(X) и числа степеней свободы r = k – v, где v – число параметров теоретического распределения плюс 1 (для нормального распределения v = 3).

Если окажется, что χ² ≤ χ²_кр, то гипотезу H следует признать верной.

Пример.

Дана гистограмма значений прочности бетона, которая аппроксимируется нормальным законом распределения. Требуется проверить правильность этой гипотезы исходя из вероятности Р =0,9.

Ri (МПа)	28-32	32-36	36-40	40-44	44-48	48-52
р ^*i	0,05	0,15	0,36	0,3	0,1	0,04

Определим среднее значение 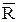и среднеквадратическое отклонение s_R.

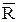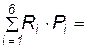=30×0,05+34×0,15+38×0,36+42×0,3+46×0,1+50×0,04≈40 МПа;

s_R = .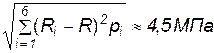

Соответствующие интервалам теоретические вероятности составят:

0,05; 0,15; 0,30; 0,30; 0,15; 0,05.

Мера расхождения:

χ² = .

Критическое значение равно χ²_кр = 0,584. Поскольку χ² < χ²_кр, гипотеза о нормальном распределении принимается.

Точечной называют оценку, которая определяется одним числом.

Интервальной называют оценку, которая определяется началом и концом некоторого интервала.

Примеры:

- по данным испытаний металла на растяжение предел текучести равен 330 МПа – точечная оценка;

- отклонения геометрических размеров сечения тоннеля от проектных лежат в интервале 0…5 см – интервальная оценка.

Надежностью (доверительной вероятностью) оценки параметра qпо его статистической характеристике q* называют вероятность g, с которой осуществляется неравенство , где характеризует точность оценки:

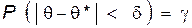. (5.8)

Обычно надежность оценки задана. Наиболее часто g принимают близкой к 1.

Пример. Нормативную прочность бетона оценивают с надежностью 0,95, расчетное сопротивление – с надежностью 0,9986.

Из формулы (5.8) вытекает понятие доверительного интервала, т.е. интервала, который покрывает неизвестный параметр q с заданной надежностью g:

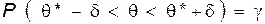(5.9)

Дата добавления: 2014-10-31