Показательное распределение

Распределение Пуассона

Если число n испытаний велико, а вероятность (p) исследуемого явления мала, используют асимптотическую формулу, так называемый закон Пуассона (закон распределения редких явлений):

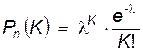(3.8)

где .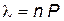

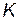Имеются специальные таблицы, пользуясь которыми можно найти , зная и .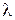

Пример.

На строительство тоннеля для возведения обделки привезли с завода 800 тюбингов. Известно, что вероятность брака на заводе составляет 0,5%. Вероятность того, что среди привезенных тюбингов будет 4 бракованных 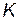, определяется по формуле (38):

;

.

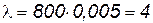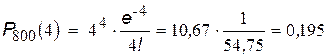Важным приложением закона Пуассона является рассмотрение случая, когда событие А в n испытаниях не произойдет ни разу, т.е. в формуле (3.8) имеем К = 0. При этом указанная формула примет вид:

P_n = e^-a. (3.9)

Представим параметр a как число отказов за промежуток времени t:

a 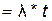, (3.10)

где 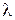- число (интенсивность) событий А в единицу времени.

Тогда вероятность ненаступления события А в течение некоторого промежутка времени t описывается показательным распределением вероятностей, которое имеет вид:

функция распределения - ;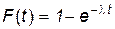

плотность распределения - 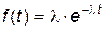, (3.11)

где 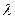- постоянная положительная величина

Показательное распределение характеризуется только одним параметром .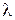

Примером распределения по показательному закону может служить время между появлениями двух последовательных событий (например, отказов, т.е. нарушений предельного состояния).

Вероятность попадания в заданный интервал показательно распределенной случайной величины равна:

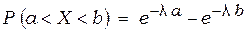. (3.12)

Функция 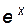- табулирована.

Числовые характеристики показательного распределения:

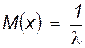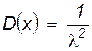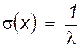; ; . (3.13)

Дата добавления: 2014-10-31