Случайная величина

Случайная величина – величина, значение которой меняется от опыта к опыту случайным образом.

Примеры: число попадание при трех выстрелах; число ошибок в тексте; уровень помехи в канале. Случайные величины обозначаются прописными буквами латинского алфавита (X, Y, Z), а значения, которые они принимают, - строчными буквами (x, y, z).

Случайные величины делятся на дискретные и непрерывные. Дискретные принимают только отдельные, изолированные значения, которые можно заранее перечислить.

Пример: число попаданий при трех выстрелах (может быть 0, 1, 2, 3). Непрерывные принимают значения, которые непрерывно заполняют некоторый промежуток.

Пример: абсцисса точки попадания при выстреле (может быть любой в интервале [ 0, r ], где r – радиус мишени).

Для математического описания случайных величин вводятся статистические характеристики:

- функция распределения вероятности;

- плотность распределения вероятности;

- математическое ожидание;

- дисперсия.

Функция распределения вероятности 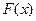– функция, которая показывает вероятность того, что все значения случайной величины не превышают некоторого заданного значения :

.

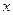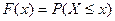Общие свойства :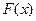

- является неубывающей (при );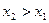

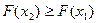- ее значения лежат в диапазоне [0, 1] ().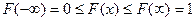

Если 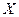- дискретная случайная величина, то 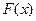- дискретная функция. Если 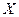- непрерывная случайная величина, то 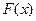- непрерывная функция;

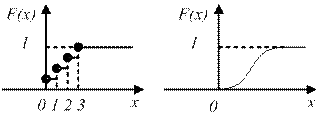
Рисунок 8.1 – Графики 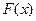для дискретной и непрерывной случайных величин.

Плотность распределения вероятности 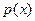представляет собой производную от функции распределения:

.

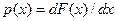Она характеризует частоту появления разных значений случайной величины при многократных наблюдениях. Чем большее значение имеет функция 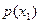, тем чаще появляются значения случайной величины 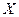, близкие к .

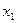Она существует только для непрерывных случайных величин.

Взаимосвязь между 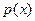и 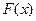определяется выражением:

.

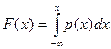Произведение 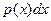представляет собой вероятность попадания значения случайной величины 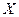в бесконечно малый интервал 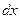в окрестности точки :

.

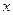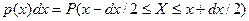Основные свойства :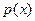

- является неотрицательной ();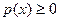

- площадь под кривой 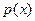всегда равна единице ();

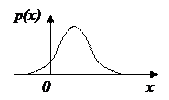
Рисунок 8.2 – График .

Для дискретной случайной величины вместо плотности распределения вероятности вводится понятие распределение вероятности, которое показывает вероятности появления всех разрешенных значений случайной величины.

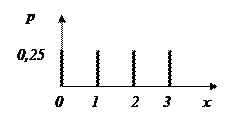
Рисунок 8.3 – Графическое изображение распределения вероятности

дискретной случайной величины.

Математическое ожидание 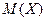или 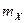представляет собой среднее значение случайной величины. Если 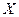– случайное напряжение (ток), то 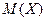- среднее значение, или постоянная составляющая, напряжения (тока).

Если 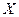- дискретная случайная величина, то при вычислении математического ожидания применяется суммирование:

,

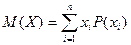где 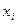- значения случайной величины;

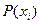- вероятности этих значений.

Если 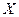- непрерывная случайная величина, то при вычислении математического ожидания применяется интегрирование:

.

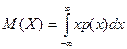Дисперсия 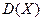или 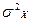характеризует степень разброса результатов отдельных опытов относительно среднего значения. Если 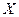– случайное напряжение (ток), то 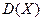- мощность переменной составляющей напряжения (тока).

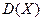вычисляется как математическое ожидание квадрата отклонения значения случайной величины от ее среднего значения. Для дискретной и непрерывной случайных величин справедливы соотношения:

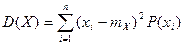и .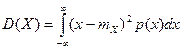

Квадратный корень из дисперсии называется среднеквадратическим отклонением:

.

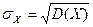В электротехнике 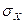- действующее (эффективное) значение случайного напряжения или тока на единичном сопротивлении.

Дата добавления: 2014-10-31