Модели межотраслевого баланса

2.1. Статическая модель линейной многоотраслевой экономики Леонтьева (модель ”затраты-выпуск”)

Эффективное функционирование экономики предполагает наличие баланса между отдельными отраслями. Каждая отрасль при этом выступает двояко: с одной стороны, как производитель некоторой продукции, с другой – как потребитель продуктов, вырабатываемых другими отраслями. Развитая математическая модель межотраслевого баланса (МОБ) появилась в 1936 году (Нобелевская премия) в трудах американского экономиста В. Леонтьева.

Рассмотрим наиболее простой вариант модели межотраслевого баланса (модель Леонтьева, или модель “затраты-выпуск”).

Алгебраическая теория анализа “затраты-выпуск” сводится к системе линейных уравнений, в которых параметрами являются коэффициенты затрат на производство продукции.

Пусть производственный сектор народного хозяйства разбит на n чистых отраслей. Чистая отрасль (это условное понятие) – некоторая часть народного хозяйства, более или менее цельная (например, энергетика, машиностроение, сельское хозяйство и т.п.).

Предположим, что каждая отрасль выпускает продукт только одного типа, и разные отрасли выпускают разные продукты. Таким образом, в рассматриваемой экономической системе выпускается п видов продуктов. В процессе производства своего вида продукта каждая отрасль нуждается в продукции других отраслей.

Пусть – количество продукции i -й отрасли, расходуемое в j -й отрасли; – объем производства i -й отрасли за данный промежуток времени, так называемый валовой выпуск продукции i; – объем потребления продукции i -й отрасли в непроизводственной сфере, объем конечного потребления; – условно чистая продукция, которая включает оплату труда, чистый доход и амортизацию.

Единицы измерения могут быть или натуральными (кубометры, тонны, штуки и т.п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы.

В табл. 2.1 отражена схема межотраслевого баланса в стоимостном выражении.

Таблица 2.1

Производящие отрасли	Потребляющие отрасли	Конечный продукт	Валовой продукт
		...	n
...	...	...	... ... ... ...	...	...	...
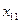
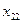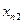
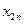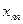
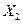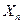
Условно чистая продукция			...
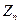
Валовой продукт			...

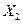
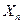
Во-первых, рассматривая схему баланса по столбцам, можно сделать очевидный вывод, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:

, j = 1, 2,..., n. (2.1)

Соотношение (2.1) охватывает систему из n уравнений, отражающих стоимостной состав продукции всех отраслей материальной сферы.

Во-вторых, рассматривая схему МОБ по строкам для каждой производственной отрасли, можно видеть, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:

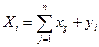, i = 1, 2,..., n. (2.2)

Формула (2.2) описывает систему из n уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования.

Балансовый характер таблицы выражается в том, что

,

.

Основу экономико-математической модели МОБ составляет матрица коэффициентов прямых затрат .

Коэффициент прямых материальных затрат показывает, какое количество продукции i -ой отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j -ой отрасли:

, i, j = 1, 2,..., n. (2.3)

Для рассмотрения модели Леонтьева сделаем два важных предположения.

1) Считаем сложившуюся технологию производства неизменной. Таким образом, матрица постоянна.

2) Предполагаем линейность существующих технологий, т.е. для выпуска j -й отраслью любого объема продукции необходимо затратить продукцию отрасли i в количестве , т.е. материальные издержки пропорциональны объему производимой продукции:

. (2.4)

Подставляя (2.4) в балансовое соотношение (2.2), получаем

(2.5)

или в матричной форме

X = A × X + Y. (2.6)

Коэффициенты прямых затрат , объемы конечного выпуска , валовые выпуски – величины неотрицательные.

С помощью этой модели можно выполнять три вида плановых расчетов.

· Задав в модели величины валовой продукции каждой отрасли (), можно определить объемы конечной продукции каждой отрасли ():

Y = (E - A) × X, (2.7)

· Задав величины конечной продукции всех отраслей (), можно определить величины валовой продукции каждой отрасли ():

X = (E - A)^-1 × Y, (2.8)

· Для ряда отраслей, задав величины валовой продукции, а для всех остальных – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

В формулах (2.7) и (2.8) Е обозначает единичную матрицу n -го порядка, а (E - A)^-1обозначает матрицу, обратную матрице (E - A). Если определитель матрицы (E - A) не равен нулю, т.е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через B =(E - A)^-1, тогда систему уравнений в матричной форме (2.8) можно записать в виде X = B × Y.

Элементы матрицы B называются коэффициентами полных материальных затрат. Они показывают, сколько всего нужно произвести продукции i -й отрасли для выпуска в сферу конечного использования единицы продукции j -й отрасли.

Плановые расчеты по модели Леонтьева можно выполнять, если выполняется условие продуктивности.

Неотрицательная матрица A называется продуктивной, если существует такой неотрицательный вектор , что

. (2.9)

Условие (2.9) означает существование положительного вектора конечной продукции для модели межотраслевого баланса (2.6).

Для того, чтобы матрица коэффициентов прямых материальных затрат A была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:

1. Матрица неотрицательно обратима, т.е. существует обратная матрица ;

2. Матричный ряд сходится, причем его сумма равна обратной матрице ;

3. Все главные миноры матрицы , т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы порядка от 1 до n, положительны.

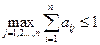Более простой, но только достаточный признак продуктивности матрицы A: максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица A продуктивна, если для любых i, j = 1, 2,..., n и , и существует номер j такой, что .

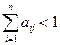Экономический смысл достаточного признака продуктивности матрицы А. Пусть А – матрица межотраслевого баланса в натурально-стоимостной форме. Другими словами, элемент матрицы показывает, на какую сумму j -я отрасль расходует продукции отрасли с номером i в расчете на 1 рубль своей продукции. Тогда величина выражает суммарную величину расхода продукции i -й отрасли (выраженную в деньгах) всеми отраслями при условии, что каждая из них выпускает объем продукции стоимостью в 1 рубль.

Очевидно, что условие , i = 1, 2,..., п, означает, что i -я отрасль способна удовлетворить запросы всех отраслей.

Таким образом, если модель Леонтьева продуктивна, то вектор валового выпуска, который необходим для удовлетворения конечного спроса Y, определяется формулой (2.8).

ГЛАВА 2. ДИНАМИЧЕСКИЕ МОДЕЛИ МАКРОЭКОНОМИКИ

Дата добавления: 2014-10-31