Медленно меняющихся внешних воздействий

Установившиеся ошибки при отработке

(коэффициенты ошибок)

Под медленно меняющимися внешними воздействиями мы будем понимать сигналы, описываемые степенными временными рядами

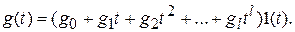
В эту группу воздействий входят почто все типовые воздействия, принятые в ТАУ для анализа и синтеза систем управления. В частности, первое слагаемое g (t) = g ₀1(t) – ступенчатое воздействие; второе слагаемое g (t) = g₀t1 (t) – скоростное (линейное) воздействие; третье слагаемое g (t) = g₀t ² 1 (t) – параболическое (квадратичное) воздействие.

Для установившейся ошибки воспроизведения медленно меняющихся воздействий было получено специальное выражение, имеющее для непрерывных систем следующую форму

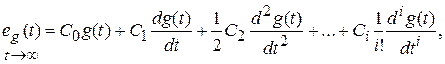
где C ₀, C ₁, C ₂, …, C_i – коэффициенты ошибок, определяемые по выражению

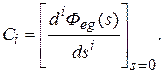
Так 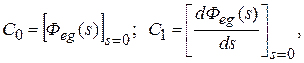где Ф_eg (s) – передаточная функция замкнутой системы по ошибке от воздействия g (t). На практике значения коэффициентов ошибок для l > 2 определяют по формулам, приведенным в справочнике. Для i =0, 1, 2 коэффициенты можно определять непосредственно по вышеприведенным формулам.

Используя выражение для установившейся ошибки через коэффициенты ошибок, найдем значение коэффициентов ошибок при отработке непрерывной системой типовых воздействий: g (t) = g ₀(t); g (t) = g ₀ t; g (t) = g ₀ t ².

1. Система статическая (порядок астатизма n = 0), воздействие ступенчатое g (t) = g ₀1(t).

Установившаяся ошибка при отработке ступенчатого воздействия

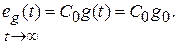
Заметим, что другие слагаемые выражения ошибки, содержащие производные от g (t) по времени будут равны нулю, так как 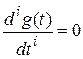при i > 0.

Коэффициент ошибки

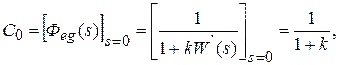
так как W ^‘(s) = 1 и значение установившейся ошибки Итак,

2. Система астатическая 1-го порядка (n = 1).

Воздействие линейное g (t) = g ₀ t1 (t).

Передаточная функция замкнутой системы по ошибке

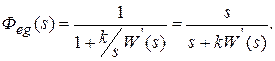
Установившаяся ошибка при отработке линейного воздействия

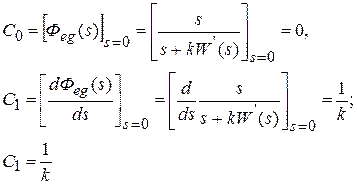
Установившееся значение ошибки 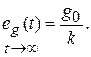Ошибка при отработке линейного внешнего воздействия называется скоростной ошибкой. Она пропорциональна скорости изменения воздействия g ₀ и обратно пропорциональна общему коэффициенту усиления разомкнутой астатической системы 1-го порядка, который называется добротностью системы по скорости.

3. Система астатическая 2-го порядка (n = 2).

Воздействие параболическое g (t) = g ₀ t ².

Передаточная функция замкнутой системы по ошибке

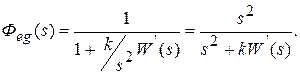
Установившаяся ошибка при отработке параболического воздействия

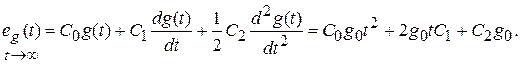
Коэффициенты ошибок

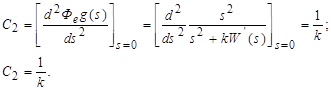Установившееся значение ошибки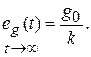

Ошибка при отработке параболического внешнего воздействия называ6ется ошибкой по ускорению. Она пропорциональна ускорению внешнего воздействия g ₀ и обратно пропорциональна общему коэффициенту передачи разомкнутой астатической системы 2-го порядка, который называется добротностью системы по ускорению.

Дата добавления: 2014-10-31