При отработке типовых степенных воздействий

Системы на установившиеся ошибки

Анализ влияния порядка астатизма

Обобщая приведенный анализ установившихся ошибок в системах различного порядка астатизма при отработке ступенчатых и медленно меняющихся воздействий, получим общие выражения установившихся ошибок в функции порядка астатизма и степени внешнего воздействия.

Пусть управляющее воздействие имеет форму , и изображения по Лапласу

Изображение ошибки при таком воздействии

.

Установившееся значение ошибки

.

Пусть передаточная функция разомкнутой системы имеет вид

,

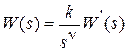где k – общий коэффициент передачи системы; n - порядок астатизма системы;
W ^’(s) – передаточная функция, не содержащая нулевых полюсов.

Тогда установившееся значение ошибки

.

Отсюда видно, что только при n > m, т. е. порядок астатизма системы n должен быть боше степени m воздействия.

При n = m установившаяся ошибка имеет постоянную величину , что означает, что системы с астатизмом 1-го и 2-го порядка будут иметь постоянные ошибки при отработке линейного и квадратичного воздействий соответственно.

При n = m = 0 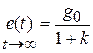. Это ошибка системы с n = 0 при отработке ступенчатого воздействия.

И, наконец, при n < m . Так система, не имеющая интеграторов, будет иметь бесконечную ошибку уже при воздействии g (t) = g₀t, т. е. при m = 1.

Сделанные выводы полностью справедливы и для дискретно непрерывной системы подобной структуры (одноконтурной). В табл. 4.2 сведены установившиеся ошибки систем (непрерывных и дискретно непрерывных) различного порядка астатизма при отработке внешних воздействий степенной формы.

Таблица 4.2

Порядок астатизма системы	Внешнее воздействие
Ступенчатое g (t) = g 01(t)	Линейное g (t) = g 0 t 1(t)	Квадратичное g (t) = g 0 t ^21(t)
n = 0
n = 1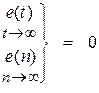
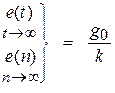
n = 2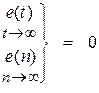

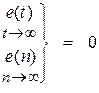
Из таблицы можно извлечь следующие выводы:

1) Система с астатизмом n = 0 (статическая система) не способна воспроизводить линейные и квадратичные сигналы и поэтому не используются как следящая или программного управления;

2) Система с астатизмом 1-го порядка (n = 1) способна работать как СПУ;

3) Система с астатизмом 2-го порядка (n = 2) обеспечивает точное воспроизведение ступенчатых и линейных сигналов и может отрабатывать квадратичные воздействия с постоянной ошибкой; может работать в режиме слежения.

Что касается установившейся ошибки от возмущающего воздействия степенной формы, то ее значение зависит не только от соотношения порядка астатизма системы и степени воздействия, но и от распределения интегрирующих звеньев между регулятором и объектом управления, т. е. зависит от точки приложения возмущающего воздействия в системе.

Пусть регулятор содержит l_p, а объект управления l ₀ интеграторов. Тогда порядок астатизма системы n = l_p + l ₀.

ПФ замкнутой системы по ошибке от возмущающего воздействия (рис. 3.22)

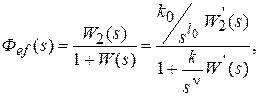
где W (s) = W ₁(s) W ₂(s) W ₃(s); причем , , ; W ₁^’(s), W ₂^’(s), W ₃^’(s) – передаточные функции, не имеющие нулевых полюсов.

Тогда

Установившееся значение ошибки от возмущающего воздействия степенной формы .

Полученное выражение позволяет сделать следующие выводы:

1. установившееся значение ошибки от возмущающего воздействия определяется соотношением числа интеграторов в регуляторе и степени воздействия и не зависит от числа интеграторов объекта управления;

2. отсутствие интеграторов в регуляторе вызывает ошибку e_f (¥) =
= f ₀ k ₀/(1 + k) при k = 0, n = 0; e_f (¥) = f ₀/ k_p при k = 0, n ¹ 0; e_f = ¥ при k ³ 1;

3. наличие интеграторов в регуляторе позволяет иметь e_f (¥) = 0 при l_p > k; e_f (¥) = f ₀/ k_p при l_p = k; e_f (¥) = ¥ при l_p < k.

Таким образом, размещения интеграторов в регуляторе до точки приложения возмущения позволяет свести к нулю ошибки установившегося режима, выбирая число интеграторов больше степени возмущающего воздействия.

Эти выводы справедливы и для дискретно непрерывной системы, в которой возмущающие воздействия приложены после регулятора.

Дата добавления: 2014-10-31