
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Взаимное положение прямой и плоскости
|
|
|
|
Вопрос 19.
Условие принадлежности точки и прямой плоскости.
Вопрос 18.
Точка принадлежит плоскости, если лежит на прямой принадлежащей плоскости
Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.
| Пусть плоскость задана пересекающимися прямыми а и b. Имеется горизонтальная проекция точки А1 необходимо построить А2. Через горизонтальную проекцию точкиа1 проведем произвольную прямую пересекающую горизонтальные проекции линий задающих плоскость в точках 1 1 и 2 1. Построим фронтальную проекцию этой линии и на ней найдем точку а 2. | 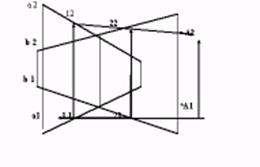
|
| Если прямая АВ параллельна прямой лежащей в некоторой плоскости, то она параллельна этой плоскости. Если необходимо через заданную точку провести прямую параллельную заданной плоскости необходимо провести в этой плоскости прямую, а затем параллельно ей через заданную точку проводят искомую прямую. Например, плоскость задана отсеком АВС и надо провести параллельную плоскости прямую через точку К. Проведем горизонтальную проекцию произвольной прямой 11 - 22, затем построим фронтальную проекцию 12 - 22. Через проекции токи К проводим линии параллельные соответствующим проекциям прямой 1 - 2. |
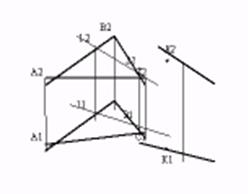
|
| Если прямая не параллельна плоскости, то она пересекает ее под тем или иным углом. Например. Отрезок DE общего положения пересекает плоскость общего положения АВС Заключаем отрезок DE во фронтально проецирующую плоскость Т. Находим проекции линии пересечения 1,2, сначала фронтальную проекцию 12, 22, а затем горизонтальную 11,21. Находим горизонтальную проекцию точки К1, а затем фронтальную К2. Для определения видимости воспользуемся конкурирующими точками 3 и 4. На горизонтальной проекции точка 31 принадлежащая прямой накладывается на точку 41 принадлежащую плоскости, однако достаточно по линии проекционной связи подняться на фронтальную плоскость проекций и видим, что точка 32 выше точки 42. Значит до точки пересечения с плоскостью прямая на горизонтальной проекции видима. | 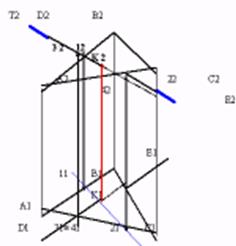
|
| Для того, чтобы прямая была перпендикулярна плоскости, она должна быть перпендикулярна по крайней мере двум прямым, лежащим в плоскости и не параллельным друг другу. Прямой угол проецируется в натуральный размер только в том случае, когда одна его сторона параллельна плоскости проекций. Поэтому достаточно в плоскости провести горизонталь и фронталь и к ним восстановить перпендикуляр, так как эти прямые проведенные из одной точки задают плоскость. Для того чтобы восстановить перпендикуляр к плоскости, необходимо, чтобы его горизонтальная проекция была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция фронтальной проекции фронтали. Горизонтали и фронтали плоскости служат для определения направления проекций перпендикуляра к плоскости. | 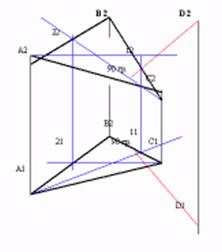
|
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 647; Нарушение авторских прав?; Мы поможем в написании вашей работы!