Преобразование импульса и энергии

Релятивистская динамика

В релятивистской динамике, так же как и в классической механике, импульс тела определяется как произведение массы на скорость. Но из условия, что фундаментальный закон сохранения импульса должен исполняться в любой инерциальной системе отсчета, выплывает, что (в отличии от классической механики) масса частицы зависит от ее скорости: (1)

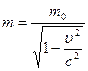
Где m₀ – масса покоя; 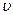- скорость частицы в системе К.

Масса частицы m называют релятивистской массой. В отличии от этой массы, масса покоя m₀ – величина инвариантная, т.е. одинаковая во всех инерциальных системах отсчета. Именно поэтому массу m₀ принимают как характеристику частицы.

Учитывая предыдущее уравнение, импульс частицы в релятивистской динамике имеет вид: (2)

При 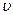<<с уравнение превращается в ньютоновское определение импульса , где m₀ не зависит от скорости (в классической механике m= m₀)

Основное уравнение релятивистской динамики.

Согласно принципа относительности Эйнштейна все законы природы должны быть инвариантными относительно инерциальных систем отсчета. Другими словами, математическая запись законов должна иметь один и тот же вид во всех этих системах. Оказывается, что в общем случае основное уравнение динамики Ньютона 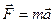не соответствует этому принципу. Вместе с этим в теории относительности доказано, что этому соответствует уравнение: (3)

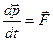
Где 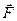- сила, которая действует на частицу. Приведенное уравнение полностью совпадает видом с основным уравнением ньютоновской динамики, но его физическое содержание отлично.

В этом уравнении слева стоит производная не от классического, а от релятивистского импульса. Совместим последние два уравнения и получим: (4)

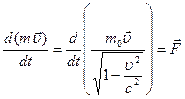
Это уравнение и есть основным уравнением релятивистской динамики. Очевидно, что именно в этом виде уравнение вызывает сохранение импульса для свободной частицы (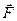 =0) и при 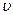<< с принимает форму основного уравнения ньютоновской динамики (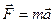, где m=m₀)

Из основного уравнения релятивистской динамики следует: вектор ускорения 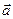частицы в общем случае не совпадает с направлением вектора силы 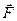. Действительно: (5)

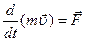
Где m – релятивистская масса.

После дифференцирования этого выражения по времени получаем: (6)

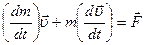
Это выражение графически изображается на рис.12, где мы видим, что вектор ускорения 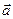не коллинеарен вектору .

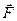Заметим, что вектор ускорения 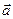сбегается с вектором силы 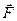только в двух случаях: вектор силы 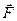перпендикулярный вектору скорости 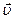(поперечная сила); вектор силы 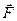параллельный вектору скорости 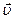(продольная сила). Поскольку в первом случае сила, которая

Рис.12действует на частицу,- продольная, она изменяет только направление скорости и не

Рис.12 изменяет саму ее величину, 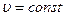. При этом условии производная 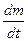в предыдущем выражении равна нулю (релятивистская масса зависит от скорости, но в данном случае 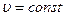, следовательно ), и уравнение приобретает вид: (7)

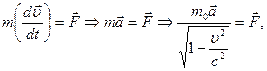
или

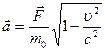
Векторы 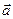и 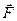совпадают по направлению.

Для случая продольной силы (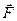 параллельно 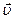) уравнение (7) имеем право просто переписать в скалярном виде. Взяв производные в левой части этого уравнения, получим: (8)

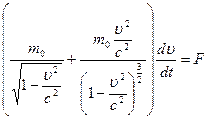
откуда: (9)

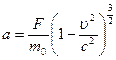
или в векторном виде

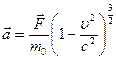
С этих выражений следует, что при одинаковых в обоих случаях значениях силы и скорости поперечная сила придает частице большее ускорение, чем продольная.

Кинетическая энергия релятивистской частицы

Определим кинетическую энергию так же как и в классической механике, а именно как величину, прирост которой равен работе силы, которая действует на частицу: (10)

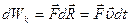
В соответствии с уравнением (3)

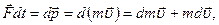
где m - релятивистская масса

Итак, принимая во внимание, что

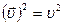, а ,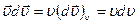

где 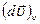- проекция вектора 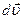на направление вектора 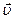, имеем (11)

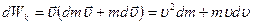
Возведем формулу(1) в квадрат и приведем ее к виду: (12)

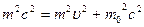
Теперь найдем дифференциал этого выражения, имея в виду, что m₀ и с - постоянные величины(13)

Разделив предыдущее выражение на 2m, получим (14)

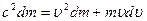
Правая часть выражения совпадает с правой частью выражения для кинетической энергии (11), то есть: (15)

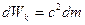
Таким образом, прирост кинетической энергии частицы пропорционален приросту ее релятивистской массы. Кинетическая энергия неподвижной частицы равна нулю, а ее масса равна m₀. Итак, проинтегрировав полученное выражение, получим (16)

или (16)

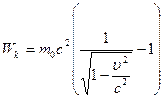
Это и есть выражение для релятивистской кинетической энергии. Если 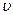<<с мы должны получить выражение для классической кинетической энергии 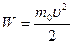. Воспользуемся формулой бинома Ньютона, согласно которой

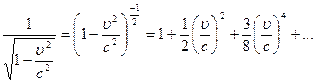
При условии 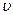<<с можно ограничиться только двумя членами ряда, и тогда выражение (16) превратится в (17)

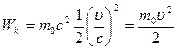
Таким образом, при 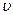<<с выражение для релятивистской кинетической энергии преобразуется в классическое выражение для кинетической энергии. Отметим, что аналогично классической механике релятивистскую кинетическую энергию нельзя представить в виде 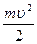, где m – релятивистская масса частицы.

Дата добавления: 2014-11-06