Б.4 Комплексный чертеж прямой линии. Прямая общего и частного положения

Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.

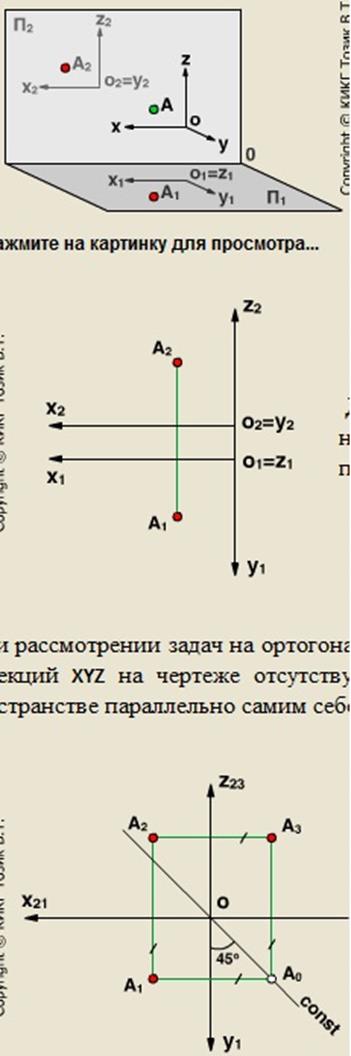Чертеж без осей проекций

В предыдущих разделах мы совместили систему ОХYZ с плоскостями проекций П1, П2 и П3: плоскостьXOY с плоскостью П1, XOZ - с П2, ZOY - с П3. Совмещение осей проекций с плоскостями проекций жестко связывает оригинал с осями координат, уделяя большее внимание при этом внешним параметрам – параметрам положения оригинала.

Оригинал вместе с системой ОХYZ будем ортогонально проецировать на плоскости проекций. Спроецируем, например, точку А вместе с системой ОХYZ на плоскости П1 иП1.

__

Две проекции объекта позволяют определить его параметры, например, точки А (А1, А2) и воспроизвести эту точку в пространстве, заданном системой ОХYZ.

__

При рассмотрении задач на ортогональном чертеже нет необходимости проводить оси проекций. Оси проекций ХYZ на чертеже отсутствуют, т.е. плоскости проекций П1, П2, П3 могут перемещаться в пространстве параллельно самим себе.

Начало координат О будет перемещаться по биссектрисе угла Х21ОZ23, которую называют постоянной прямой чертежа. Ее можно задать произвольно, либо сначала построить третью проекцию А3, а затем провести биссектрису угла А1А0А3.

Б.3. Основные свойства (инварианты) проецирования.

При параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин), причём степень нарушения зависит как от аппарата проецирования, так и от положения проецируемой геометрической фигуры в пространстве по отношению к плоскости проекции.
Но наряду с этим, между оригиналом и его проекцией существует определённая связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Эти свойства называются инвариантными (проективными) для данного способа проецирования.
Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.

Основными и неизменными его свойствами (инвариантами) являются следующие:

1) проекция точки – точка;

2) проекция прямой – прямая;

3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

Частный случай центрального проецирования – параллельное проецирование, когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.4). В этом случае полученное изображение называют параллельной проекцией объекта.

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

1. проекции параллельных прямых параллельны между собой;

2. отношение отрезков прямой равно отношению их проекций;

3. отношение отрезков двух параллельных прямых равно отношению их проекций.

Прямоугольное (ортогональное) проецирование является частным случаем параллельного.

Проекция объекта, полученная с использование этого метода, называется ортогональной.

Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.

Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.

Прямые частного положения - это прямые, параллельные одной или двум плоскостям проекций.

В первом случае прямые называются прямыми уровня.

Во втором случае - проецирующими прямыми, т.к. перпендикулярны какой-нибудь плоскости проекций.

Прямая общего пололожения- называют прямую, не параллельную ни одной из данных плоскостей проекций. Любой отрезок такой прямой проецируется в данной системе плоскостей проекций искаженно. Искаженно проецируются и углы наклона этой прямой к плоскостям проекций.

Дата добавления: 2014-11-06