Теорема

Теорема

Если плоскости α и β взаимно перпендикулярны, и к плоскости α проведен перпендикуляр, имеющий общую точку с плоскостью β, то этот перпендикуляр лежит в плоскости β.

Пусть плоскости α и β перпендикулярны плоскости γ и пересекаются по прямой a, тогда a 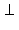γ.

Доказательство

Чертеж 3.3.4.

На прямой a выберем произвольную точку A (чертеж 3.3.4). Проведем через точку A перпендикуляр к плоскости γ. По теореме 3.9 этот перпендикуляр лежит в каждой из плоскостей α, β, следовательно, он лежит на линии их пересечения.

Б16. Способ перемены плоскостей проекций.

Сущность- положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система П₂⁄П₁ дополняется плоскостями, образующими с П₂ или 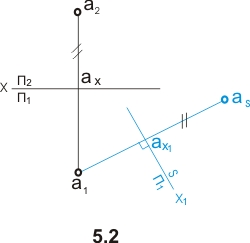П₁, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение, наиболее удобное для выполнения требуемого построения.

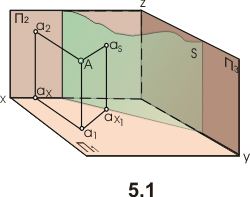
На рис. 5.1 показано преобразование проекций точки А из системы П₂⁄П₁ в систему S⁄П₁, в которой вместо плоскости П₂ введена новая плоскость S, а плоскость П₁ осталась неизменной. При этом S перпендикулярна П₁. В системе S⁄П₁ горизонтальная проекция a точки A осталась неизменной. Проекция a_s точки A на плоскости S находится от плоскости П₁ на том же расстоянии, что и проекция a₂ точки А на плоскости П₂. Это условие позволяет легко строить проекцию точки на чертеже (рис.5.2) на новой плоскости проекций. Для этого в новой системе (П₁⁄S) из проекции точки (a) на сохраняющейся плоскости проекций проводят линию связи, перпендикулярную к новой оси проекций (S / П₁). На этой линии связи отмечают расстояние от оси П₁ / S до проекции a_s точки на новой плоскости проекций S, равное расстоянию от преобразуемой проекции точки a₂ до оси проекций П₂/ П₁ в системе П₂[П₁ (| a_s-a_x1| =| a₂- a_x |).

В дальнейшем, при введении новой плоскости проекций, ось проекций можно обозначать в виде дроби, черта которой лежит на оси; каждую букву при этом пишут как бы на ′своей′ плоскости.

Проекции точек на новых плоскостях проекций удобно отмечать индексами плоскости (например, a_s, b_t и т. д.).

Перемену плоскостей проекций можно производить последовательно несколько раз.

Дата добавления: 2014-11-06