Пересечение сферы и тора плоскостью. Пример построения линии среза на поверхности тела вращения сложной формы

Рис. 9.10 Рис. 9.11

Пересечение сферы плоскостью. Плоскость всегда пересекает сферу по окружности, которая проецируется в виде отрезка пря­мой, в виде эллипса или в виде окружности в зависимости от поло­жения секущей плоскости по отношению к плоскости проекции.Так, на рисунке 9.10 изображены проекции линий пересечения сферы и плоскостей горизонтальной Р (P_v) и фронтальной S (S_h). Они

пересекают сферу по окружности с центрами С (с', с, с") и Q (с'_и с_и с") с проекциями в виде окружности и отрезка прямой. В примере, приведенном на рисунке 9.11, горизонтальная и про­фильная проекции линии пересечения сферы фронтально-про­ецирующей плоскостью — эллипсы, длины больших осей которых сd и c"d" равны величине диаметра окружности (а'Ъ'). Малые оси эллипсов аЬи а"Ъ "получают проецированием. На рисунке 9.11 показано построение проекций некоторых точек. Проекции с и d построены на горизонтальной проекции параллели радиуса о—1, построенной с помощью проекции Г. Проекции с"и d" построены на профильной проекции окружности, проведенной на сфере через проекции с' {d') так, что плоскость окружности параллельна плоскости проекций. Проекция е является точкой касания эллипса (горизонтальной проекции окружности среза) и экватора сферы. Она построена в проекционной связи на гори­зонтальной проекции экватора по фронтальной проекции е'. Го­ризонтальная проекция т произвольной точки на линии среза построена с помощью параллели радиуса о —2, фронтальная про­екция которой проходит через проекции т' и 2'. Проекция /" является точкой касания эллипса (профильной проекции окруж­ности среза) и профильной проекции очерка сферы.

Если плоскость, пересекающая сферу, является плоскостью общего положения, то задачу решают способом перемены плоскос­тей проекций. Дополнительную плоскость проекций выбирают так, чтобы обеспечить перпендикулярность ее и секущей плоско­сти. Это позволяет упростить построение линии пересечения.

Линию пересечения тора плоскостью в общем случае строят при помощи вспомогательных плоскостей, пересекающих тор и секущую плоскость. При этом подбирают плоскости, пересе­кающие тор по окружности, т. е. расположенные перпенди­кулярно оси тора или проходящие через его ось.

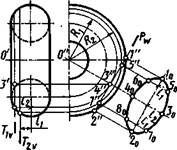
В примере на рисунке 9.12 показано применение вспомога­тельных плоскостей Т\ {T_iv) и Т_г (T_lv), перпендикулярных к оси тора, для построения линии пересечения и натурального вида фигуры сечения поверхности тора плоскостью Р (Р_ш). Тор на рисунке 9.12 имеет два изображения — фронтальную проекцию и половину профильной проекции. Полуокружность радиуса Рц (про­фильная проекция линии пересечения тора вспомогательной плос­костью 71) касается проекции плоскости Р (следа Р_ш). Тем самым определяются профильная проекция 3" (o"3"LP_w) и по ней —

Рис. 9.12

фронтальная проекция 3 'одной из точек проекции искомой линии пе­ресечения. Полуокружность радиу­са R₂ — профильная проекция линии пересечения тора вспомогательной плоскостью Т₂. Она пересекает про­фильную проекцию плоскости Р (след P_w) в двух точках 5" и 7'-профильных проекциях точек линии пересечения. Проводя аналогичные построения, можно получить необ­ходимое количество проекций точек для искомой линии пересе­чения. Используем найденные точки для построения натуральной величины сечения. Фигура сечения тора плоскостью, парал­лельной его оси, имеет оси и центр симметрии. При ее постро­ении использованы расстояния h и /₂ на фронтальной проекции для нанесения точек 5q, 7₀ и 3₀. Точки 6₀, 8₀ и 4₀ построены как симметричные. Построенная кривая пересечения поверхности тора плоскостью выражается алгебраическим уравнением 4-го порядка.

Кривые пересечения тора с плоскостью, параллельной оси, приведены на рисунке 9.13. Они имеют общее название — кривые Персея (Персей — геометр Древней Греции). Это кри­вые 4-го порядка. Вид кривых зависит от расстояния секущей плоскости до оси тора.

1Г

Кривые Персея
Б-Б В-В

Многие детали приборов и машин имеют в своей основе форму тела вращения со сложной формой поверхности. Такое тело можно рассматривать как состоящее из частей элементар­ных тел вращения — щшиндра, конуса, сферы и тора или круго­вого кольца. Детали из такого тела вращения часто конструируют путем среза части тела плоскостью, параллельной оси. При этом в пересечении поверхности тела с плоскостью среза образуют­ся сложные линии, построение которых и рассмотрено ниже. Эти линии, являющиеся частным случаем линии пересечения поверхности вращения с плоскостью (плоскость параллельна оси), называются линиями среза.

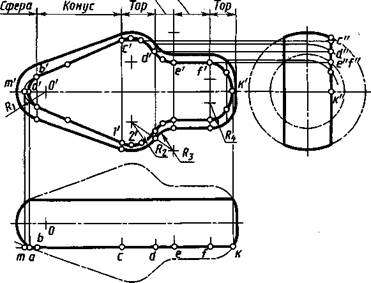
Пример чертежа тела вращения с построенными линиями среза приведен на рисунке 9.14. На чертеже оставлены некоторые вспомогательные линии построений и точки. При выполнении построений прежде всего устанавли­вают границы заданных поверхностей вращения и определяют элементарные поверхности: цилиндр, конус, сфера, тор. Для этого достаточно мысленно или на черновике дополнить участки поверхностей, как показано на рисун­ке 9.15. (На рисунке все составляющие поверхности для наглядности раздви­нуты вдоль оси вращения.)

Разграничение участков элементарных поверхностей позволяет опреде­лить характер отдельных участков линий среза и правильно выбрать число и

Рис. 9.14

Гор Цилиндр

расположение вспомогательных секущих плоскостей, необходимых для пост­роения промежуточных точек на линии среза.

На чертеже границами поверхностей вращения являются линии Касания или пересечения элементарных поверхностей. Их проекции в виде отрезков прямых, перпендикулярных к оси вращения, проводят через проекции то­чек сопряженния или пересечения образующих. Так, на рисунке 9.14 грани­ца между сферой и конусом проведена через точку сопряжения дуги радиуса J?i и образующей конуса. Эта точка определена с помощью перпендикуляра из проекции О'центра сферы к образующей конуса. Граница между конусом и тором с радиусом образующей Л₂ проведена через точку касания образую­щей конуса и дуги радиуса Л₂. Тоска сопряжения определена с помощью перпендикуляра, проведенного из центра дуги радиуса Л₂ к образующей ко­нуса. Граница между тором с радиусом образующей Л₂ и тором с радиусом образующей Л₃ проведена через точку сопряжения дуг с радиусами Л₂ и Л₃-Точка сопряжения найдена с помощью прямой, соединяющей центры дуг. Границы между тором с радиусом образующей Л₃ и цилиндром, между этим же цилиндром и тором с радиусом образующей R* проведены через точки сопряжения дуг указанных радиусов с образующей цилиндра.

Построенные границы элементарных поверхностей можно рассматривать и как линии пересечения поверхности вращения плоскостями, перпендику­лярными оси, в данном случае профильными плоскостями. Профильные проекции этих линий — окружности. В пересечении их с профильными проекциями плоскостей среза отмечают профильные проекции характерных точек на линии среза. Пример построения профильной проекции d" и по ней фронтальной проекции *Г отмечен на рисунке 9.14. По положению про­екции d", с", е ", f" строят фронтальные проекции d\ с', t\ /' точек линии среза. Проекции а', к' (их проекции а", к" совпадают) построены по гори­зонтальным проекциям а, к.

В данном примере линия среза и ее фронтальная проекция состоят из следующих участков: на сфере радиуса R_x — дуги окружности радиуса а 'о '; на

конусе — части гиперболы с вершиной т'\ на торе с радиусом образующей Л₂ — части кривой Персея, аналогичной кривой сечения А—А (см. рис. 9.13); на торе с радиусом образующей Л₃ — части кривой Персея, ана­логичной кривой сечения В—В (см. рис. 9.13); на цилиндре — отрезков прямых, параллельных оси; на торе с радиусом образующей R* — части кри­вой Персея, аналогичной кривой сечения Г—Г (см. рис. 9.13). Зная вид линии среза и положение проекций характерных и крайних точек линий, можно ограничиться построением проекций минимального числа промежу­точных точек. На рисунке 9.14 показаны построения проекций промежуточ­ных точек на участках k'f', b'c', c'd', d'e'. Следует отметить, что точка Г симметрична точке с' а точка 2' наиболее удалена от оси. Справа от точки 2' указана точка, симметричная точке V.

(Пример детали с линией среза см. на рисунке 16.11.)

Дата добавления: 2014-11-06