Распределение капитальных вложений

Задача коммивояжера

Задача о ранце

Задача составления смесей

Транспортная задача

Задача о назначениях

Формирование производственной программы

Рассмотрим производственный участок, выпускающий два типа деталей. Исходная заготовка при изготовлении деталей первого типа проходит две операции (токарную и сверлильную) при трудоемкости 20 и 30 ч/шт. соответственно. При изготовлении детали второго типа необходимы три операции (токарная, сверлильная, шлифовальная) при трудоемкости 40, 30, 20 ч/шт. соответственно. Прибыль от продажи деталей равна 1,5 руб./шт. для деталей первого типа и 1 руб./шт. для деталей второго типа.

На плановый период ресурс рабочего времени по операциям в часах составляет: токарная – 1000, сверлильная – 900, шлифовальная – 400 ч. Необходимо подобрать производственную программу выпуска деталей, обеспечивающую максимальную прибыль.

Обозначим количество деталей первого типа, принимаемых для выпуска, через y, второго типа – х. Математическая постановка задачи определения у и х имеет вид

40 х + 20 у = 1000;

30 х + 30 у = 900;

20 х = 400;

х > 0, y > 0;

J = 1,5 y + 1 x → max.

Пусть имеются n работ и n кандидатов для их выполнения. Назначению i – го кандидата (i = 1… n) на j – ю работу (j = 1… n) соответствуют определенная эффективность (прибыль, производительность) или затраты какого‑либо ресурса Требуется назначить на выполнение всех видов работ таких кандидатов, которые обеспечат наибольшую эффективность, т. е. минимум суммарных затрат или максимум прибыли (производительности). Каждого кандидата можно назначить только на одну должность, и каждая работа может быть выполнена только одним кандидатом.

Математическая постановка задачи имеет вид:

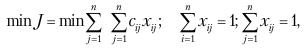
где x_j – искомая переменная: X_j = 1, если i – й кандидат распределяется на j – ю работу; 0 – в противном случае.

В такой постановке данная задача относится к классу комбинаторных.

Транспортная задача – это задача о выборе плана перевозок однородного продукта из пунктов производства в пункты потребления. Пусть имеется m пунктов отправления и n пунктов назначения. Ресурсы продукта в пунктах отправления обозначим через a (i), потребность в продукте в пункте потребления – b (j). Расходы на доставку единицы продукта от поставщика i к потребителю j равняются c (i, j). Балансовое условие производства и потребления имеет вид:

a (1) + a (2) +… + a (n) = b (1) + b (2) +… + b (m).

Требуется определить x (i, j) – количество продукта, доставляемое от пункта производства i к пункту потребления j. Обязательными условиями являются:

необходимость вывоза всего произведенного продукта:

x(i, 1) + x(i, 2) +… + x (i, m) = a(i) для всех значений i;

необходимость удовлетворения всех потребителей:

x (1, j) + x (2, j) +.·· + x (n, j) = b (j) для всех значений j.

Оптимальный план доставки продукта должен обеспечить минимум общей суммы затрат на доставку:

Решаются транспортные задачи методами линейного программирования.

Задачи составления рациона корма, состава шихты при выплавке стали, состава цементной смеси относятся к группе задач составления смесей. В такой задаче задается набор исходных материалов, характеризующихся содержанием контролируемых компонентов а(i,j) – содержание i – го компонента в j – м виде исходного материала.

Требуется определить x (j) – количество j – го материала, принимаемого для подготовки комплексной смеси. Совокупность ограничений включает условия вида:

x (j) < X (j);

x (1) + x (2) +… + x(n) < Y;

a(i, 1) x (1) + a(i, 2) x (2) +… + a(i, n) x(n) > A(i).

Здесь X (j) – допустимое для использования количество j – го материала, Y – общее ограничение на массу исходного материала, A (i) – минимально необходимое содержание i – го компонента в конечном продукте.

Оценкой вариантов решения задачи является сумма затрат на состав материалов в формируемой смеси:

J = c (1) x (1) + c (2) x (2) +… + c (n) x (n),

где c (j) – расходы на единицу j – го материала.

Пусть имеется некоторый объем V, который необходимо заполнить различными предметами. Предметов имеется несколько видов, отличающихся объемом v (i) и ценностью c (i).

Требуется определить вариант заполнения предметами объема V, чтобы их суммарная ценность оказалась наибольшей. Неизвестные переменные задачи – это x (i) – число предметов i – го вида, выбранных для размещения в ранце. Ограничения задачи имеют вид:

x (1) v (1) + x (2) v (2) +… + x (n) v (n) < V;

x (i) > 0.

Оценка вариантов решения задачи – это сумма

J = x (1) c (1) + x (2) c (2) +… + x (n) c (n),

которая должна иметь максимальное значение.

Обычно эта задача формулируется следующим образом. Коммивояжер должен побывать в ряде городов. Известны расстояния между каждой парой городов (время или стоимость проезда). Необходимо выбрать кратчайший маршрут, проходящий один раз через каждый город. Если расстояние между городами не зависит от направления движения, то задача называется симметричной. Если стоимость проезда меняется при изменении направления движения, задача называется несимметричной.

Для задачи коммивояжера при необходимости посещения только двух городов выбора нет. При посещении трех городов и заданном начальном пункте возможны 2 маршрута. Если городов четыре, то имеется 6 маршрутов, а при одиннадцати городах – более 3,5 млн допустимых маршрутов. В общем случае при n городах имеется (n ‑1)! маршрутов.

К подобному типу задач сводится множество реальных ситуаций. Например, выбор очередности обработки разнородных изделий, маршрута автотранспорта, задачи выбора маршрута в сетях систем связи.

Пример. Пусть имеется 5 пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт. Известно время перевозки из пункта i в пункт j (табл. 7.1).

Таблица 7.1

Время переезда, ед.

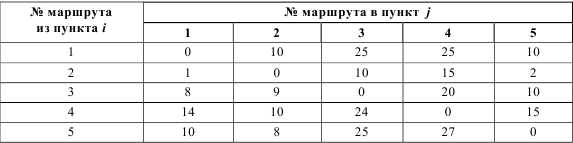
Требуется найти маршрут с наименьшей продолжительностью, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда.

Решение. Введем обозначения: i и j – номера пунктов выезда и въезда; t. – время переезда из пункта i в пункт j. В общем случае t_ij может быть не равно времени переезда в обратном направлении

– t_ij ≠ t_ji (например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевы переменные:

Составим модель (рис. 7.1). Из пункта 1 можно выехать в любой из пунктов: 2, или 5, или 3, или 4, или остаться в пункте 1. Но при этом можно выехать только в одном‑единственном направлении. Это условие можно записать так:

δ₁₁ + δ₁₂ + δ₁₃ + δ₁₄ + δ₁₅ = 1

Эти зависимости обеспечивают выполнение условия, согласно которому из каждого пункта выезд производится только один раз и только в одном направлении.

Условие въезда в пункт 1 аналогично условию выезда из пункта 1. Требование минимальной продолжительности маршрута запишется в виде целевой функции:

min L = t₁₁δ₁₁+ t₁₂δ₁₂ + t₁₃δ₁₃ + t₁₄δ₁₄ + t₁₅δ₁₅ + t₂₁δ₂₁ + t₂₂δ₂₂ +… + t₅₅δ₅₅

где t_ij берутся из исходной таблицы, а δ_ij – искомые переменные.

Математическую постановку задачи можно сформулировать в виде:

В результате решения системы получим следующие значения (рис. 7.2):

δ₁₁⁰ = δ₅₂⁰ = δ₂₃⁰ = δ₃₄⁰ = δ₄₁⁰ = 1, остальные δ_ij⁰ = 0;

min L = 10 + 8 + 10 +20 + 14 = 62.

Рис. 7.2

Переходя от частной постановки к общей, задачу коммивояжера можно сформулировать так:

Пусть известны возможные значения эффективности (например, прирост прибыли, выпуск продукции и др.) на каждом из четырех предприятий отрасли в результате расширения действующих мощностей (табл. 7.2).

Требуется составить план распределения ограниченных капиталовложений по этим предприятиям (К = 200 ден. ед.), максимизирующий общий прирост выпуска при заданной номенклатуре и структуре отраслевого плана производства продукции.

Таблица 7.2 Возможные значения эффективности предприятий в результате расширения действующих мощностей

Решение.

Данная задача может быть решена методом динамического программирования. Обозначим: g i (x) – прирост выпуска продукции на i – м предприятии при x единиц капиталовложений на реконструкцию или расширение активной части его основных фондов; F (K) – максимально возможный прирост выпуска продукции при распределении суммы К между четырьмя предприятиями.

Тогда, согласно основному функциональному уравнению Беллмана:

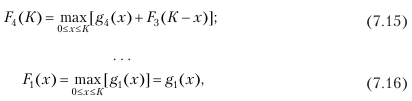
т. е. максимальный прирост выпуска продукции на первом предприятии при распределении для него (и только для него) единиц капиталовложений x (0 ‹x ‹K) будет соответствовать значениям графы 2 исходных данных.

Реализация задачи будет заключаться в последовательном решении уравнений Беллмана, описывающих максимальный прирост выпуска при распределении К = 200 между двумя предприятиями, затем тремя и четырьмя. В процессе вычислений x меняется от 0 до К с шагом Δ = 50:

и т. д. (табл. 7.3).

Из анализа результатов расчетов следует, что наибольший достижимый прирост продукции составит

F₄ (200) = g₄ (150) + F₃ (50) = 110 + 36 = 146,

т. е. четвертому предприятию должно быть выделено 150, а первым трем – 50 ед. средств.

Таблица 7.3

т. е. все оставшиеся 50 ед. выделяются третьему заводу.

Итак, решение задачи: x₁⁰ = x₂⁰ = 0; x₃⁰ = 50; x₄⁰= 150ден. ед.

Дата добавления: 2014-11-20