Метод Лагранжа. Вся совокупность методов решения управленческих задач делится на две группы: аналитические и численные

Вся совокупность методов решения управленческих задач делится на две группы: аналитические и численные. При выборе метода решения конкретной задачи следует учесть, что аналитическое решение всегда предпочтительнее численного, так как оно позволяет исследовать влияние различных факторов на оптимальное решение. Однако при решении практических задач не всегда удается получить аналитическое решение.

Общего метода решения всех управленческих задач не существует.

В зависимости от вида оценки вариантов решения задачи, состава и вида ограничивающих условий могут применяться различные методы поиска оптимального решения. Иногда одна задача может решаться разными методами. Аналитические методы решения управленческих задач опираются на дифференциальное исчисление. Наиболее универсальными среди численных методов являются методы линейного и динамического программирования. Для численных методов решения необходимо иметь четкую область ограничений. Чем меньше эта область, тем проще поиск оптимального решения.

Дифференциальное исчисление – метод поиска оптимального решения через вычисление производных оптимизируемой функции. Для отыскания экстремума (максимума, минимума) функции одной переменной J (x) необходимо найти решение уравнения

dJ / dx = 0.

Если вторая производная меньше нуля, то имеет место максимум функции, если вторая производная больше нуля, то имеет место минимум функции.

В случае функции нескольких переменных задача оптимизации сводится к решению систем уравнений, каждое из которых является производной по одной из переменных.

Необходимым условием применения метода дифференциального исчисления является дифференцируемость выражения J(x) и в общем случае – отсутствие ограничений.

Метод Лагранжа – метод дифференциального исчисления, применяемый при наличии ограничивающих условий. Этот метод позволяет перейти от оптимизационной задачи с ограничениями к альтернативной оптимизационной задаче без ограничений при совпадении решений. Фактически математическая задача на условный экстремум заменяется задачей на безусловный экстремум, но с увеличением числа неизвестных.

Первоначальная задача:

с(x) → min;

A(x) > 0.

Альтернативная задача:

с(x) + λA(x) → min.

Условиями экстремума при решении данной задачи являются условия равенства нулю производной по x и λ.

Коэффициент λ называется множителем Лагранжа. Если в исходной задаче имеется набор ограничений, то в альтернативной задаче во втором слагаемом появляется сумма слагаемых с коэффициентами λ(i). Если ограничение по i – му ресурсу в точке экстремума обращаются в равенство, то множитель Лагранжа для них не равен нулю. Если ограничения в точке экстремума не оказывают влияние на решение, то множитель Лагранжа для них равен нулю.

При общей постановке оптимизационной задачи в виде

max (min) f (x₁, x₂…, x_n); g_i (x₁, x₂…, x_n) = b_i (i =1… m),

функция Лагранжа имеет вид:

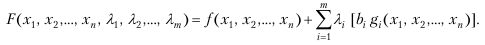
Для ее оптимизации находят частные производные

и рассматривают систему n + m уравнений:

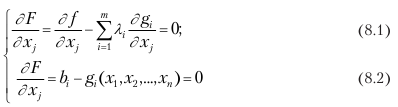
с n + m неизвестными x₁, x₂…., x_n, λ₁, λ₂…, λ_m.

Всякое решение системы определяет точку x = (x₁⁰, x₂⁰…, x⁰_n), в которой может иметь место экстремум функции f (x₁, x₂…, x_n) Следовательно, решив систему уравнений, получим все точки, в которых функция Лагранжа может иметь экстремальные значения.

Пример. Известен рыночный спрос на определенное изделие в количестве 180 шт. Это изделие может быть изготовлено двумя предприятиями одного концерна по различным технологиям. При производстве x 1 изделий первым предприятием его затраты составят 4x₁ + x₁² руб., а при изготовлении x 2 изделий вторым предприятием – 8x₂ + x₂² руб. Требуется определить, сколько изделий, изготовленных по каждой технологии, может предложить концерн, чтобы общие издержки его производства были минимальны.

Решение. Запишем математическую постановку задачи в виде:

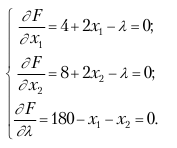
Для нахождения минимального значения целевой функции составим функцию Лагранжа

F (x₁, x₂, λ) = 4x₁ +x₁² + 8x₂ + x₂² + λ(180 – x₁ – x₂),

вычислим ее частные производные по x₁, x₂, λ и приравняем их к нулю:

Отсюда 4 + 2x₁ = 8 + 2x₂, или x₁ + x₂ = 2. Решая это уравнение совместно с x₁ + x₂ = 180, находим x₁⁰ =91; x₂⁰=89, т. е. получаем координаты точки, подозрительной на экстремум. Используя вторые частные производные, можно показать, что в этой точке функция f имеет условный минимум.

Дата добавления: 2014-11-20