Виды и методы измерений

Классификация видов измерений приведена на рис. 1.4. Виды измерений определяются физическим характером измеряемой ве­личины, требуемой точностью измерения, необходимой скорос­тью измерения, условиями и режимом измерений и т.д. Из рис. 1.4 следует, что в метрологии существует множество видов измерений и число их постоянно увеличивается. Можно, например, выделить виды измерений в зависимости от их цели: контрольные, диагно­стические и прогностические, лабораторные и технические, эта­лонные и поверочные, абсолютные и относительные и т.д.

Наиболее часто используются прямые измерения, состоящие в том, что искомое значение величины находят из опытных данных путем экспериментального сравнения. Например, длину измеря­ют непосредственно линейкой, температуру – термометром, силу – динамометром. Уравнение прямого измерения: у = Сх, где С – цена деления СИ.

Если искомое значение величины находят на основании изве­стной зависимости между этой величиной и величинами, най­денными прямыми измерениями, то этот вид измерений называ­ют косвенным. Например, объем параллелепипеда находят путем умножения трех линейных величин (длины, ширины и высоты); электрическое сопротивление – путем деления падения напря­жения на величину силы электрического тока. Уравнение косвен­ного измерения

у = f (х ₁ х ₂, …, х_n),

где x_i – i -й результат прямого измерения.

Совокупные измерения осуществляются путем одновременного измерения нескольких одноименных величин, при которых иско­мое значение находят решением системы уравнений, получаемых в результате прямых измерений различных сочетаний этих вели­чин. При определении взаимоиндуктивности катушки M, напри­мер, используют два метода: сложения и вычитания полей. Если индуктивность одной из них L ₁, а другой – L ₂, то находят L ₀₁,= L ₁ + L ₂ + 2 M и L ₀₂, = L ₁ + L ₂ – 2 M. Откуда М = (L ₀₁ – Z ₀₂)/4.

Совместными называют производимые одновременно (прямые и косвенные) измерения двух или нескольких неодноименных ве­личин. Целью этих измерений, по существу, является нахождение функциональной связи между величинами. Например, измерение сопротивления R ₁ проводника при фиксированной температуре t по формуле

R ₁ = R _o (1+αΔ t),

где R_о и α – сопротивление при известной температуре t_o (обычно 20 °С) и температурный коэффициент – величины постоянные; измеренные косвенным методом; Δ t = t – t_o – разность температур; t – заданное значение температуры, измеряемое прямым мето­дом.

Приведенные виды измерений включают различные методы, т.е. способы решения измерительной задачи с теоретическим обо­снованием и разработкой использования средств измерения по принятой МВИ. Методика – это технология выполнения измерений с целью наи­лучшей реализации метода.

Прямые измерения – основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29–99 различают:

1. Метод непосредственной оценки, при котором значение ве­личины определяют непосредственно по отсчетному устройству измерительного прибора, например, измерение давления пружин­ным манометром, массы – на весах, силы электрического тока – амперметром.

2. Метод сравнения с мерой, где измеряемую величину сравни­вают с величиной, воспроизводимой мерой. Например, измере­ние массы на рычажных весах с уравновешиванием гирей; изме­рение напряжения постоянного тока на компенсаторе сравнени­ем с ЭДС параллельного элемента.

3. Метод дополнения, если значение измеряемой величины до­полняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее за­данному значению.

4. Дифференциальный метод характеризуется измерением раз­ности между измеряемой величиной и известной величиной, вос­производимой мерой. Метод позволяет получить результат высо­кой точности при использовании относительно грубых средств измерения (рис. 1.5).

Рис. 1.5. Дифференциальный метод измерения

Пример 1.2. Измерить длину х стержня, если известна длина L (L < х)меры. Как показано на рис. 1.5, х = l + а (а – измеряемая величина).

Действительные значения а_д будут отличаться от измеренного а на величину погрешности Δ:

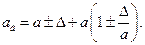
Тогда

Поскольку l >> а, то <<

Пусть Δ = 0,1 мм; l = 1000 м; а = 10 мм. Тогда

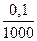= 0,0001 (0,01 %) << 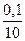= 0,01 (1 %).

5. Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины. Рассмотрим, например, неравноплечие весы (рис. 1.6, а), где Р ₁ l ₁= Р ₂ l ₂. В электротехнике – это мосты для измерения индуктивности, емкости, сопротивления (рис. 1.6, б). Здесь r ₁ r ₂ = r_xr ₃, откуда r_x = r ₁ r ₂/ r ₃. В общем случае совпаде­ние сравниваемых величин регистрируется нуль-индикатором (И).

Рис. 1.6. Нулевой метод измерения: а – схема механических весов;
б – схема электрического моста

6. Метод замещения – метод сравнения с мерой, в которой измеряемую величину замещают известной величиной, воспро­изводимой мерой. Например, взвешивание с поочередным поме­щением измеряемой массы и гирь на одну и ту же чашку весов.

Кроме того, можно выделить нестандартизованные методы:

¨ метод противопоставления, при котором измеряемая вели­чина и величина, воспроизводимая мерой, одновременно воздей­ствуют на прибор сравнения. Например, измерения массы на рав­ноплечих весах с помещением измеряемой массы и уравновеши­вающих ее гирь на двух чашках весов;

¨ метод совпадений, где разность между сравниваемыми вели­чинами измеряют, используя совпадение отметок шкал или пе­риодических сигналов.

Например, при измерении длины штангенциркулем наблюда­ют совпадение отметок на шкалах штангенциркуля и нониуса; при измерении частоты вращения стробоскопом – метки на вращаю­щемся объекте с момента вспышек известной частоты.

В литературе [2; 43; 18] иногда встречается название измере­ний с однократными наблюдениями – обыкновенные измере­ния, а с многократными – статистические. Кроме того, если весь измеряемый параметр фиксируется непосредственно СИ, то это – абсолютный метод, а если СИ фиксирует лишь отклонение пара­метра от установочного значения, то это относительный (порого­вый) метод измерения.

Другие виды и методы измерений (см. рис. 1.4) не требуют специальных пояснений и будут рассмотрены ниже.

Дата добавления: 2014-11-25