Погрешности измерений

При практическом использовании тех или иных измерений важно оценить их точность. Термин «точность измерений», т.е. степень при­ближения результатов измерения к некоторому действительному зна­чению, не имеет строгого определения и используется для качествен­ного сравнения измерительных операций. Для количественной оцен­ки используется понятие «погрешность измерений» (чем меньше погрешность, тем выше точность). Оценка погрешности измерений – одно из важных мероприятий по обеспечению единства измерений.

Количество факторов, влияющих на точность измерения, дос­таточно велико, и любая классификация погрешностей измере­ния (рис. 1.7) в известной мере условна, так как различные по­грешности в зависимости от условий измерительного процесса проявляются в различных группах. Поэтому для практических целей достаточно рассмот-

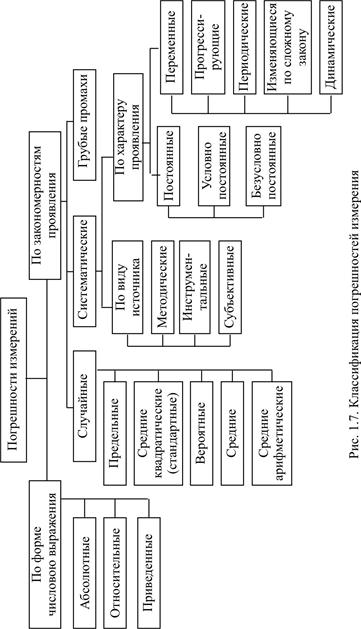
реть случайные и систематические состав­ляющие общей погрешности, выраженные в абсолютных и отно­сительных единицах при прямых, косвенных, совокупных и рав­ноточных измерениях.

Погрешность измерения Δ x – это отклонение результата из­мерения х от истинного (действительного) х _и(х _д) значения изме­ряемой величины:

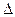x _изм = x – x _д.

В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность определяется как разность результата измерения и истинного значения измеряемой величины Δ = х – х _иили Δ = х – х _д, а относительная – по формуле

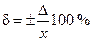или .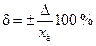

Приведенная погрешность 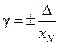100 %, где х_N – нормированное значение величины. Например, х_N = х _max, где х _max – максималь­ное значение измеряемой величины.

В качестве истинного значения при многократных измерениях параметра выступает среднее арифметическое значение х,

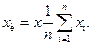(1.6)

Величина х, полученная в одной серии измерений, является случайным приближением к х _и. Для оценки ее возможных откло­нений от х _и определяют опытное среднее квадратическое откло­нение (СКО),

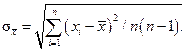(1.7)

Для оценки рассеяния отдельных результатов х измерения от­носительно среднего х определяют СКО:

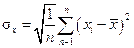при n ≥ 20,

(1.8)

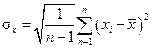при n ≤ 20.

Примечание. Применение формул (1.3) правомерно при усло­вии постоянства измеряемой величины в процессе измерения. Если при измерении величина изменяется, как при измерении темпе­ратуры остывающего металла или измерении потенциала провод­ника через равные отрезки длины, то в формулах (1.8) в качестве х следует брать какую-то постоянную величину, например нача­ло отсчета.

Формулы (1.7) и (1.8) соответствуют центральной предельной теореме теории вероятностей, согласно которой

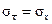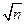/ . (1.9)

Среднее арифметическое из ряда измерений всегда имеет мень­шую погрешность, чем погрешность каждого определенного из­мерения. Это отражает и формула (1.9), определяющая фундамен­тальный закон теории погрешностей. Из него следует, что если необходимо повысить точность результата (при исключенной си­стематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз, и т.д.

Нужно четко разграничивать применение 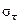и σ _x: величина 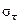используется при оценке погрешностей окончательного результата, а σ _x – при оценке погрешности метода измерения.

В зависимости от характера проявления, причин возникнове­ния и возможностей устранения различают систематическую и случайную составляющие погрешности измерений, а также гру­бые погрешности (промахи).

Систематическая Δ _c составляющая остается постоянной или закономерно изменяется при повторных измерениях одного и того же параметра.

Случайная Δ _s составляющая изменяется при повторных изме­рениях одного и того же параметра случайным образом.

Грубые погрешности (промахи) возникают из-за ошибочных дей­ствий оператора, неисправности средств измерения или резких изменений усло­вий измерений. Как правило, грубые погрешности выявляются в результате обработки результатов измерений с помощью специ­альных критериев.

Случайная и систематическая составляющие погрешности из­мерения проявляются одновременно, так что общая погрешность при их независимости

Δ = Δ _c + Δ _s

или через СКО

σ_Δ = 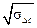+ σ_{Δ s} .

Значение случайной погрешности заранее неизвестно, оно воз­никает из-за множества неуточненных факторов.

Случайные погрешности нельзя исключить полностью, но их влияние может быть уменьшено путем обработки результатов из­мерений. Для этого должны быть известны вероятностные и стати­стические характеристики (закон распределения, закон математи­ческого ожидания, СКО, доверительная вероятность и довери­тельный интервал). Часто для предварительной оценки закона распределения параметра используют относительную величину СКО – коэффициент вариации:

υ _х = σ/ х или υ _х = (σ/ х)100 %. (1.10)

Например, при υ < 0,33…0,35 можно считать, что распреде­ление случайной величины подчиняется нормальному закону. Если Р означает вероятность а, т.е.того, что х результата измерения отличается от истинного на величину не более чем Δ_s, т.е.

Р = а { x – Δ _s < x_и < x + Δ _s }, (1.11)

то в этом случае Р – доверительная вероятность, а интервал от x – Δ _s до x + Δ _s – доверительный интервал. Таким образом, для характеристики случайной погрешности надо обязательно задать два числа – величину самой погрешности (или доверительный интервал) и доверительную вероятность.

Если распределение случайной погрешности подчиняется нормальному закону (а это, как правило), то вместо значения Δ _s ука­зывается σ _x. Одновременно это уже определяет и доверительную вероятность Р. Например: при Δ = σ _x значение Р = 0,68; при Δ = 2σ _x значение Р = 0,95; при Δ = 3σ _x значение Р = 0,99.

Доверительная вероятность по формуле (1.11) характеризует вероятность того, что отдельное измерение х не будет отклонять­ся от истинного значения более чем на Δ. Безусловно, важнее знать отклонение от истинного значения среднего арифметичес­кого ряда измерений.

До сих пор рассматривались оценки СКО по «необходимому» (достаточно большому) числу измерений. В этом случае σ² называет­ся генеральной дисперсией. При малом числе измерений (менее 10–20) получают так называемую выборочную дисперсию σ². Причем σ²→ σ² лишь при n → ∞. То есть если считать, что σ² = σ², то надежность оценки уменьшается с уменьшением п, а значения до­верительной вероятности P завышаются. Поэтому при ограниченном числе измерений п вводят коэффи­циент Стьюдента t, определяемый по специальным таблицам в за­висимости от числа измерений и принятой доверительной ве­роятности Р.

Тогда средний результат измерений находится с заданной вероят­ностью Р в интервале J = х ± t σ _x 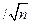и отличается от действитель­ного значения на относительную величину ε = Δ/σ _x =Δ 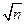/σ _x.

Для уменьшения случайной погрешности есть два пути: повы­шение точности измерений (уменьшение σ _x) и увеличение числа измерений п с целью использования соотношения (1.9). Считая, что все возможности совершенствования техники измерений использо­ваны, рассмотрим второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью опре­деляться систематической составляющей Δ _c. Если систематическая погрешность определяется классом точности СИ Δ_си (или γ_си), то необходимо, чтобы доверительный интервал ± t_p σ _x 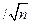был суще­ственно меньше Δ _c.

Обычно принимают от Δ _s ≤ 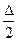до Δ _s ≤ 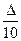при Р = 0,95.

В случае невозможности выполнить эти соотношения необходимо коренным образом изменить методику измерения. Для сравнения случайных по­грешностей с различными законами распределения использование показателей, сводящих плотность распределения к одному или не­скольким числам, обязательно. В качестве таких чисел и выступают СКО, доверительный интервал и доверительная вероятность.

Надежность самого СКО характеризуется величиной 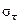= σ 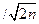принято, что если 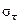< 0,25, то оценка точности надежна. Это условие выполняется уже при п = 8.

Для практических целей важно уметь правильно сформулиро­вать требования к точности измерений. Например, если за допус­тимую погрешность изготовления принять Δ = 3σ, то, повышая требования к контролю (например, до Δ = σ), при сохранении технологии изготовления увеличивается вероятность брака.

Наиболее вероятная погрешность Δ_в отдельного измерения определяется по формуле

Δ_в= 0,67 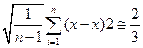σ.

Анализ этой формулы показывает, что с увеличением п вели­чина Δ_в быстро уменьшается лишь до п = 5…10. Следовательно, увеличение числа измерений на одном режиме свыше 5…10 неце­лесообразно, что совпадает с условием получения надежных зна­чении σ_σ.

Число измерений можно выбрать из данных табл. 1.5 или по одной из формул:

n = (t _p σ_x,/0,5Δ_c)²;

n ≥ 2(1 – n _от)/(1 – Р),

где п _от – число отбрасываемых экспериментальных результатов. С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения как
δ _i = t_p σ _x / x среднего зна­чения δ _x = t_p σ _x / х .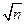

Таблица 1.5

Необходимое число измерений при нормальном законе распреде­ления случайной величины (при Р = 0,95)

Относительная погрешность, δ	Коэффициент вариации, υ
0,20	0,25	0,30	0,35
0,05
0,10
0,15		13 13
0,20
0,25

Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях пол­ностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то неисключенные остатки, ко­торые и нужно учитывать, чтобы оценить их границы. Это и будет определением результатов измерения.

Оставшаяся необнаруженной систематическая составляющая опаснее случайной: если случайная составляющая вызывает вари­ацию (разброс) результатов, то систематическая – устойчиво их искажает (смещает). В любом случае отсутствие или незначитель­ность (с целью пренебрежения) систематической погрешности нужно доказать.

Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей. Методика выявления характера погрешности заключается в следующем:

1. Из двух рядов 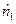и 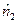независимых измерений находят средние арифметические х ₁ и х ₂.

2. Определяют значения

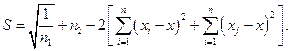
3. Вычисляют σ =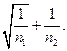

4. Вероятность того, что разность | х ₁ – х ₂|≥ε является случай­ной величиной, определяется равенством

Р (| х ₁ – х₂|)≥ ε) = 1 – P_tp.n,

где 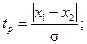n = n ₁ +n _{2 –}2.

Величина Р определяется по таблице Стьюдента.

Если полученная вероятность Р > 0,95, то разность | х ₁ – х ₂| носит систематический характер.

Пример 1.3. Расчетные значения составили t = 3
и п = 15. По таблице Стьюдента находим, что при
п – 1 = 14 и t – 2,98 = 3 вели­чина Р = 0,99. Тогда Р = 0,99 > 0,95, что свидетельствует о система­тическом характере погрешности.

В отличие от случайной погрешности, выявленной в целом вне зависимости от ее источников, систематическая погрешность рас­сматривается по составляющим в зависимости от источников ее воз­никновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.

Субъективные систематические погрешности связаны с инди­видуальными особенностями оператора. Как правило, эта погреш­ность возникает из-за ошибок в отсчете показаний (примерно 0,1 деления шкалы) и неопытности оператора. В основном же систе­матические погрешности возникают из-за методической и инст­рументальной составляющих.

Методическая составляющая погрешности обусловлена несо­вершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая возникает из-за собствен­ной погрешности средств измерения, определяемой классом точности, влия­нием средств измерения на результат и ограниченной разрешающей способ­ности средств измерения.

Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие определяется следующими моментами:

¨ для повышения точности измерений можно выделить лими­тирующие факторы, а следовательно, принять решение об усо­вершенствовании методики или выборе более точных средств измерения;

¨ появляется возможность определить составляющую общей погрешности, увеличивающейся со временем или под влиянием внешних факторов, а следовательно, целенаправленно осуществ­лять периодические поверки и аттестации;

¨ инструментальная составляющая может быть оценена до раз­работки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляю­щая.

Следовательно, все виды составляющих погрешности нужно анализи­ровать и выявлять в отдельности, а затем суммировать их в зави­симости от характера, что является основной задачей при разра­ботке и аттестации методик выполнения измерений.

В ряде случаев систематическая погрешность может быть исключе­на за счет устранения источников погрешности до начала измерений (профилактика погрешности),
а в процессе измерений – путем внесе­ния известных поправок в результаты измерений.

Профилактика погрешности – наиболее рациональный способ ее снижения и заключается в устранении влияния, например, тем­пературы (термостатированием и термоизоляцией), магнитных по­лей (магнитными экранами), вибраций и т.п. Сюда же относятся регулировка, ремонт и поверка средств измерения.

Исключение постоянных систематических погрешностей в про­цессе измерений осуществляют методом сравнения (замещения, противопоставления), компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематичес­кая погрешность входила с разным знаком), а исключение пере­менных и прогрессирующих – способами симметричных наблюде­ний или наблюдением четное число раз через полупериоды.

Пример 1.4. Пусть периодическая погрешность меняется по закону

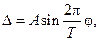
где φ – независимая величина, от которой зависит Δ (время, угол поворота и т.д.); Т – период изменения погрешности.

Пусть при φ = φ_о величина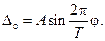

Находим значение погрешности для φ = φ_o + ε, где ε – такой интервал, при котором

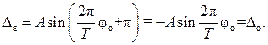
Определим, чему равен интервал ε.

Решение. По условию для интервала ε имеем

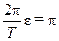и ε = T/ 2.

В этом случае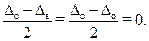

То есть периодическая погрешность исключается, если взять сред­нее двух наблюдений, произведенных одно за другим через интер­вал, равный полупериоду независимой переменной φ, определяю­щей значение периодической погрешности. То же будет и для не­скольких пар подобного рода наблюдений (например, погрешность от эксцентриситета в угломерных средствах измерения).

Краткое содержание главы

Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. Метрология базируется на комплексе терминов и понятий, главные из которых таковы.

Физическая величина – свойство, в качественном отношении общее для многих физических объектов, но в количественном отношении для каждого объекта индивидуальное. Физическими величинами являются длина, масса, плотность, сила, давление и другие.

Единица физической величины – числовое значение этой величины, равное 1. Например, масса 1 кг, сила 1 Н, давление 1 Па.

Единицы одной физической величины в различных системах единиц могут различаться по размеру, например для силы 1 кг и 10 Н.

Значение физической величины – численная оценка физической величины конкретного объекта в принятых единицах. Например, значение массы кирпича – 3,5 кг.

Техническими измерениями называется определение значений различных физических величин специальными техническими методами и средствами. При лабораторных испытаниях используют измерения геометрических размеров, массы, температуры, давления, силы и другие. Важнейшие требования, предъявляемые к техническим измерениям, – единство и точность измерений.

Единство измерений – состояние измерений, когда их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью. Единство измерений необходимо, чтобы можно было сопоставлять результаты измерений, выполненные в разных местах, в различное время, с помощью разнообразных приборов.

Точность измерений – качество измерений, отражающее близость результатов к истинному значению измеряемой величины.

Значение физической величины 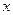_изм, полученное при измерении, находят по формуле

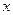_изм= А / n,

где А – числовое значение; n – единица физической величины. В метрологии различают истинное и действительное значения физических величин.

Истинное значение физической величины идеальным образом отражает в качественном отношении соответствующие свойства объекта. Истинное значение свободно от ошибок измерения. Поскольку все значения физической величины находят опытным путем и они содержат ошибки измерений, то истинное значение остается неизвестным.

Действительное значение физической величины находят экспериментальным путем; оно настолько приближается к истинному значению, что для определенных целей может быть использовано вместо него. При технических измерениях значение физической величины, найденное с допустимой техническими требованиями погрешностью, принимают за действительное значение.

Погрешность измерения – отклонение результата измерений от истинного значения измеряемой величины. Поскольку истинное значение измеряемой величины остается неизвестным, на практике лишь приближенно оценивают погрешности измерений, сравнивая результаты измерения со значением этой же величины, полученным с точностью в несколько раз более высокой. Например, погрешность измерения размеров образца линейкой, которая составляет 1 мм, можно оценить, измерив образец штангенциркулем с погрешностью не более 0,05 мм. Различают погрешность абсолютную, выражаемую в единицах измеряемой величины, и относительную, представляющую собой отношение абсолютной погрешности к действительному значению измеряемой величины.

Средства измерений – технические средства, используемые при измерениях и имеющие нормированные метрологические свойства. Средства измерений делят на меры и измерительные приборы.

Мера – средство намерения, предназначенное для воспроизведения физической величины заданного размера (например, гиря – мера массы).

Измерительный прибор – средство измерений, которое служит для воспроизведения измерительной информации в форме, доступной для восприятия наблюдателем. Простейшие измерительные приборы (например, линейка, штангенциркуль) называют измерительным инструментом.

Основные метрологические показатели приборов:

– цена деления шкалы – разность измеряемой величины, соответствующая двум соседним отметкам шкалы;

– начальное и конечное значения шкалы – соответственно наименьшее и наибольшее значения измеряемой величины, указанные на шкале; диапазон измерений – область значений измеряемой величины, для которой нормированы допускаемые погрешности.

Погрешности измерения – результат взаимного наложения ошибок, вызываемых различными причинами: погрешностью самих измерительных приборов, погрешностями, возникающими при пользовании прибором и считывании результатов измерений и погрешностей из-за несоблюдения условий измерения.

При достаточно большом числе измерений среднее арифметическое результатов измерений приближается к истинному значению, а погрешность уменьшается.

Иногда при измерениях возникает так называемая грубая погрешность измерения, которая существенно повышает погрешность, ожидаемую при данных условиях. Результаты измерений, содержащие грубые погрешности, исключают из рассмотрения как недостоверные.

Средства измерений выбирают таким образом, чтобы их допускаемая погрешность в заранее установленных условиях применения, т.е. с учетом всех дополнительных погрешностей, не превышала погрешности, установленной стандартом или техническими условиями (ТУ) на данный вид измерения (испытания) материала. Применять средства измерения, погрешность которых значительно ниже требуемой стандартом, нерационально, особенно при комплексном испытании материала, когда другие измерения проводятся с большей погрешностью. Например, измерение массы и объема пробы материала при расчете его плотности нужно выполнять средствами измерения, имеющими приблизительно одинаковую погрешность.

Единство измерений обеспечивается установлением единиц измерений и разработкой их эталонов. На XI генеральной конференции по мерам и весам (1960) была принята Международная система единиц (СИ), которая заменила сложную совокупность систем единиц и отдельных внесистемных единиц, сложившихся на основе метрической системы мер. В России СИ принята в качестве стандартной, а в области строительства ее применение регламентировано СН 528-80 «Перечень единиц физических величин, подлежащих применению в строительстве». Переход на новую систему единиц в условиях сложного хозяйства нашей страны в короткие сроки невозможен, поэтому до настоящего времени в части технической документации, в шкалах приборов и аппаратов используют старые единицы физической величины.

Допуск – допускаемое отклонение числовой характеристики какого-либо параметра от его номинального (расчетного) значения в соответствии с заданным классом точности. Допуск задают на геометрические размеры деталей и изделий, на механические, физико-химические и другие величины (например, прочность, твердость, химический состав).

Допуски указывают в стандартах, технических требованиях или чертежах изделий в виде двух предельных размеров (наибольшего и наименьшего), между которыми находится действительный размер, т.е. размер, определяемый измерением. Вместо предельных размеров в технической документации обычно указывают номинальный размер, полученный при расчетах данного изделия, и два предельных отклонения – верхнее и нижнее, равные соответственно алгебраической разности наибольшего и наименьшего предельных размеров и номинального размера. Например, при определении стандартной консистенции гипсового теста (ГОСТ 23789–79) диаметр расплыва теста должен быть (180–5) мм; отклонение размеров керамического кирпича по длине составляет не более – 5 мм, а по ширине – 4 мм (ГОСТ 530–2007).

Допуски устанавливают для поддержания необходимого качества материалов, изделий и взаимозаменяемости деталей и сборочных единиц машин, аппаратов и сооружений.

Взаимозаменяемость – свойство одинаковых деталей и сборочных единиц, позволяющее производить сборку или заменять их без предварительной подгонки. Взаимозаменяемость имеет большое народно-хозяйственное значение и является одной из предпосылок организации массового и крупносерийного производства

В строительстве проблема взаимозаменяемости особенно остро встала в связи с развитием сборного строительства, когда различные детали и сборочные единицы одного здания или сооружения производятся различными предприятиями. В этом случае эффективная сборка здания возможна лишь при обеспечении взаимозаменяемости и соблюдении требуемых допусков.

Измерение – это сравнение исследуемой величины с другой однотипной величиной, принятой за единицу измерения.

Истинного значения измеряемой величины мы не получаем никогда. Результаты измерений дают лишь ее приближенное значение. Это связано с природой измеряемых объектов и с принципиальной невозможностью абсолютно точных измерений.

Различные измерительные приборы дают возможность получить значение измеряемой величины с той или иной степенью точности. Точность прибора – его свойство, характеризующее степень приближения показаний этого прибора к действительному значению измеряемой величины. Точность прибора зависит от физического явления, на основе которого построен метод измерения, а также от точности изготовления отдельных частей прибора (допуски).

Все погрешности измерений делят на два типа: систематические и случайные.

В основе теории случайных ошибок лежат два предположения, подтвержденные опытом:

1. При большом количестве измерений ошибки одинаковой величины, но разного знака встречаются с одинаковой частотой.

2. Вероятность появления ошибки тем меньше, чем больше ее абсолютная величина.

В процессе исследования материалов, особенно в тех случаях, когда преследуется цель – установить, чем влияние некоторого фактора на свойства материала, получаемого в одном эксперименте, отличается от влияния на свойства такого же материала, полученного в другом эксперименте.

При бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерения.

Нормальное распределение отклонений от истинного значения характеризуется двумя параметрами: генеральным средним значением случайной величины и дисперсией.

Для оценки границ доверительного интервала используют коэффициент, который называют «коэффициентом (критерием) Стьюдента».

Для оценки точности измерений введено понятие относительной ошибки, равной отношению абсолютной ошибки результата измерений к среднему значению измеряемой величины.

Для оценки измеряемой величины вычисляют средние значения ее, которые оценивают с помощью среднего квадратического значения и взвешенного среднего.

В процессе исследования материалов, особенно в тех случаях, когда преследуется цель – установить, чем влияние некоторого фактора на свойства материала, получаемого в одном эксперименте, отличается от влияния на свойства такого же материала, полученного в другом эксперименте. Для решения этого вопроса необходимо выяснить, является ли расхождение средних значимым или находится в пределах ошибки эксперимента. Устанавливают значимость расхождения средних значений с помощью критерия Стьюдента.

Математическое описание эмпирических зависимостей, полученных в экспериментах, производят с помощью метода наименьших квадратов (МНК).

Дата добавления: 2014-11-25