Последовательный колебательный

.

.

Таким образом, простейший ФНЧ вида рис. 3.7 обладает низкой избирательностью, не зависящей от его параметров.

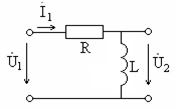Проведем аналогичный анализ простейшего фильтра верхних частот, схема которого показана на рис. 3.11. Его комплексный коэффициент передачи равен

.

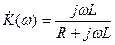Для модуля (АЧХ) и аргумента (ФЧХ) получим

Рис. 3.11

,

,

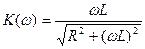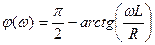Их графики, построенные пр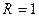и кОм и 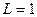мГн, показаны на рис. 3.12а и рис. 3.12б соответственно.

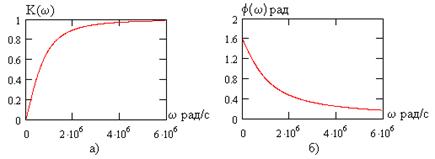
Рис. 3.12

Как видно, цепь является фильтром верхних частот. Для расчета полосы удержания удобнее представить АЧХ в виде выражения

.

Его максимум 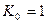, тогда из (3.1) получим уравнение

,

из которого получим выражение для полосы пропускания,

.

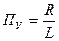Для расчета коэффициента прямоугольности (3.6) определим полосу удержания 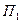на уровне 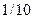от максимума как решение уравнения вида

,

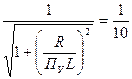тогда полос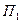а равна

.

Согласно (3.6), коэффициент прямоугольности равен

И в этом случае простой фильтр верхних частот имеет низкую избирательность.

3.4. Апериодические фильтры второго порядка

В фильтрах второго порядка присутствуют два реактивных элемента, при этом возможны следующие варианты:

- реактивные элементы одного типа (или две емкости, или две индуктивности);

- реактивные элементы разного типа (индуктивность и емкость).

Фильтры с одинаковыми реактивными элементами называют апериодическими. Их работа основана на зависимости от частоты реактивных сопротивлений индуктивностей или емкостей.

В качестве примера рассмотрим RC фильтр нижних частот второго порядка, схема которого показана на рис. 3.13.

При известном зна-

Рис. 3.13 чении входного напряже-

ния 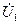методом узловых напряжений определим выходное напряжение 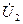, схема цепи с необходимыми обозначениями показана на рис. 3.14. Выразим токи ветвей через узловое напряжение ,

,

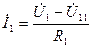Рис. 3.14

,

.

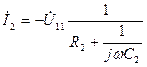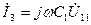По первому закону Кирхгофа 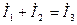получим уравнение

,

решением которого является узловое напряжение

,

или после преобразований

.

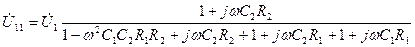Зная , нетрудно определить выходное напряжение,

.

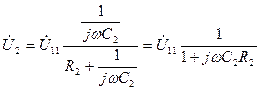Подставляя , получим

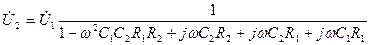
и комплексный коэффициент передачи будет равен

.

Годограф 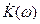(КЧХ цепи) показан на рис. 3.15.

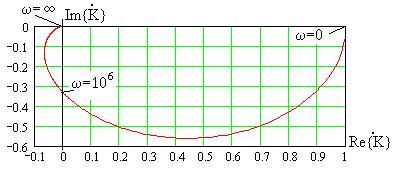
Рис. 3.15

Определим АЧХ 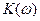рассматриваемого фильтра как модуль ,

.

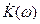График АЧХ показан на рис. 3.16, а та же зависимость в децибелах - на рис. 3.17, ФЧХ фильтра приведена на рис. 3.18 пр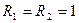и кОм и 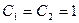нФ. Пунктиром на рис. 3.16 изображена АЧХ простого ФНЧ вида рис. 3.6а.

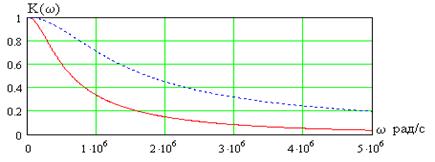
Рис. 3.16

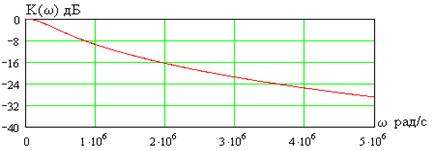
Рис. 3.17

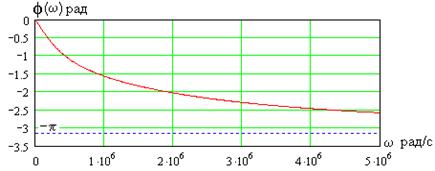
Рис. 3.18

Найдем полосу пропускания фильтра . Максимум АЧХ равен 1, тогда получим уравнение

.

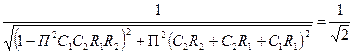Его решение имеет вид (получите его самостоятельно)

,

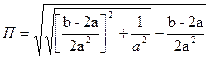где введены обозначения

.

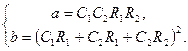В частном случае при и получим

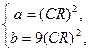
при этом полоса пропускания равна

.

Как видно из полученной формулы и из графиков АЧХ на рис. 3.16, рассматриваемый ФНЧ второго порядка имеет меньшую полосу пропускания, чем простейший ФНЧ вида рис. 3.6а при одинаковых величинах 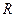и .

Вычислим коэффициент прямоугольности ФНЧ на рис. 3.13. Для этого определим полосу пропускания 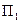на уровне 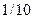от максимума, равного 1, из уравнения вида

.

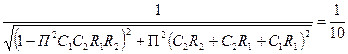Решая его аналогично предыдущему, получим

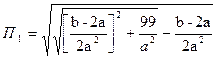
и коэффициент прямоугольности равен

,

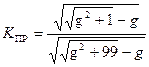где

.

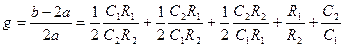Обозначим отношения сопротивлений и емкостей фильтра соответственно

тогда получим

.

Зависимость 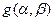показана на рис. 3.19а, а на рис. 3.19б – зависимость коэффициента прямоугольности от параметра .

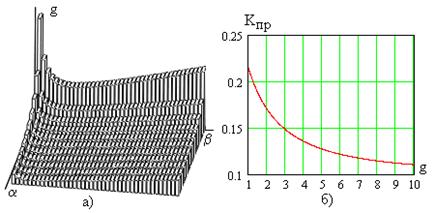
Рис. 3.19

Для определения оптимальных параметров фильтра найдем значение 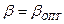, при котором обеспечивается минимум функции 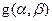, решая уравнение

,

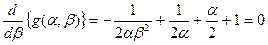результат имеет вид

.

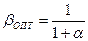Чем больше 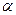, тем меньше оптимальное значение 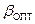и выше коэффициент прямоугольности.

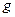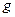Определим минимально достижимое значение параметра , для чего подставим в выражение для и найдем предел при (проделайте это самостоятельно). В результате получим, что величина 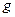не менее 1. Зависимость при 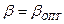показана на рис. 3.20а, а на рис 3.20б – зависимость от 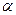коэффициента прямоугольности.

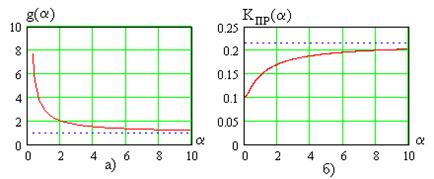
Рис. 3.20

Величина увеличивается с падением 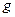и при 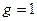() принимает наибольшее значение

.

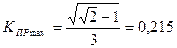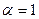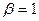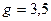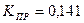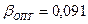Для одинаковых значений сопротивлений () и емкостей () получим и , что заметно меньше максимального значения. Для получим и коэффициент прямоугольности .

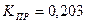На рис. 3.21 показаны АЧХ фильтра при и 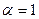(пунктирная линия), а на рис 3.22 – те же зависимости в децибелах. Как видно, при увеличении 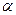АЧХ затухает быстрее в области верхних частот, то есть уменьшается полоса пропускания 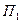на уровне 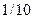от максимума АЧХ, за счет этого повышается коэффициент прямоугольности.

Рассматриваемый RC фильтр нижних частот второго порядка вида рис. 3.13 обеспечивает коэффициент прямоугольности более 0,2, что в два раза выше, чем у простейшего ФНЧ.

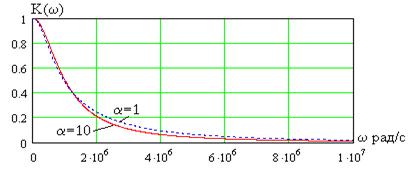
Рис. 3.21

Рис. 3.22

Приведенный анализ характеристик RC фильтра второго порядка может рассматриваться как пример для исследований в рамках курсовой работы.

3.5. Фильтры второго порядка типа LC

Если фильтр второго порядка построен на элементах L и C, то его работа может быть основана на зависимости от частоты их реактивных сопротивлений, или на явлениях резонанса тока или напряжения в этих элементах (в этом случае цепь назыв а ют резонансной). В таких цепях всегда присутствуют активные сопротивления 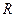(дискретные резисторы или сопротивления потерь в реактивных элементах).

Апериодические LC фильтры характеризуются включенными в них большими активными сопротивлениями R и их свойства подобны выявленным при анализе апериодических RC цепей. Резонансные LC цепи будут рассмотрены в дальнейшем.

3.6. Задания для самостоятельного решения

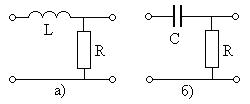Задание 3.1. Определите комплексные коэффициенты передачи фильтров, показанных на рис. 3. 23. Постройте графики КЧХ. Получите выражения для их АЧХ и ФЧХ, постройте графики, получите выражения для полосы пропускания и коэффициента прямоугольности.

Рис. 3.23

Задание 3.3. Получите выражения для АЧХ и ФЧХ фильтров с учетом сопротивления нагрузки , соответствующие схемы показаны на рис. 3.24.

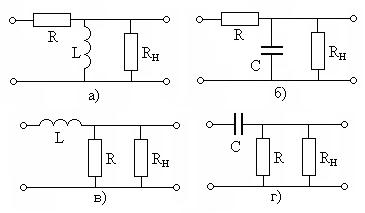
Рис. 3.24

Исследуйте влияние нагрузки на частотные характеристики и полосу пропускания фильтра.

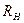Задание 3.3. Определите АЧХ и ФЧХ показанных на рис. 3.25 фильтров, постройте их графики. Получите выражение для коэффициента прямоугольности с учетом сопротивления нагрузки . Исследуйте влияние на частотные характеристики и избирательность этих фильтров.

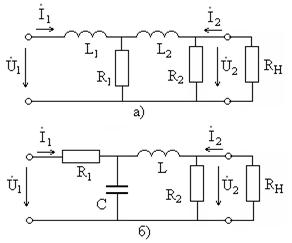
Рис. 3.25

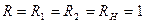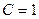Задание 3.4. Получите частотные характеристики цепей из заданий 3.1 - 3.3 с помощью программы схемотехнического моделирования при кОм, нФ и 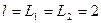мГн, определите полосы пропускания, с помощью режима «Stepping» исследуйте влияние нагрузки на их АЧХ и ФЧХ.

Дата добавления: 2014-11-25