Основные понятия теории цепей 1 страница

ВВЕДЕНИЕ

Курс общей электротехники является базовым для различных специальностей, на него опираются другие профилирующие дисциплины. Он охватывает материал основ теории линейных и нелинейных электрических цепей. В него включены элементы теории трехфазных и магнитных цепей, теории электрических измерений.

Помимо теоретических знаний при освоении материала необходимо приобрести навыки решения задач по соответствующим разделам (этому направлению в учебном пособии уделяется особое внимание), овладеть основами техники измерений.

Современная вычислительная техника предоставляет широкие возможности по моделированию электрических цепей (пакеты программ WorkBench, MicroCAP, OrCad и другие). Это направление подготовки специалистов имеет большое самостоятельное значение и является хорошим вспомогательным средством при изучении электрических цепей и сигналов в ходе аудиторных занятий и самостоятельной работы. К учебному пособию прилагаются примеры программ, которые можно получить у преподавателя.

Изучение общей электротехники базируется на курсах алгебры и высшей математики и раздела «Электричество и магнетизм» курса физики.

По курсу имеется учебная литература, например [1-3], с широким и глубоким охватом материала. В предлагаемом учебном пособии достаточно кратко излагаются основные разделы курса общей электротехники, отобран материал по узловым вопросам, обеспечивающим базовую подготовку с упором на практическое применение и, прежде всего, решение основных типов задач. Для углубленного изучения необходимо обратиться к учебникам [1-3] и задачникам [4,5].

1.1. Электрическая цепь

Описание работы и расчет (моделирование) электрических устройств можно проводить на базе теории электромагнитного поля. Этот подход приводит к сложным математическим моделям (системам дифференциальных уравнений в частных производных) и используется в основном при анализе сверхвысокочастотных устройств и антенн.

Значительно проще и удобнее моделировать электрические устройства на основе уравнений электрического равновесия токов и напряжений. На этой основе построена теория электрических цепей.

1.2. Заряд, ток, напряжение, мощность, энергия

Электрическим зарядом называют источник электрического поля, через которое заряды взаимодействуют друг с другом [3]. Электрические заряды могут быть положительными (ионы) и отрицательными (электроны и ионы). Разноименные заряды притягиваются, а одноименные – отталкиваются. Величина заряда измеряется в кулонах (К).

Величина (сила) тока равна отношению бесконечно малого заряда (количества электричества) 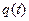, переносимого в данный момент времени 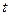через поперечное сечение проводника за бесконечно малый интервал времени 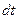к величине этого интервала,

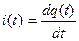. (1.1)

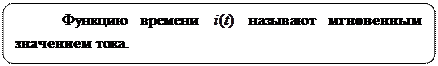
Ток измеряется в амперах (А), в технике широко используют значения в миллиамперах (1 мА=10^-3 А), микроамперах (1 мкА=10^-6 А) и наноамперах (1 нА=10^-9 А), значения дольных приставок приведены в приложении 1.

Электрический потенциал 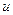некоторой точки – это величина, равная отношению потенциальной энергии 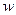, которой обладает заряд 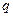в этой точке, к величине заряда,

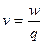. (1.2)

Потенциальная энергия 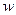равна энергии, затрачиваемой на перенос заряда из данной точки с потенциалом 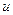в точку с нулевым потенциалом.

Если 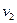- потенциал точки 2, а 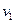- точки 1, то напряже-

ние между точками 2 и 1 равно

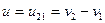. (1.3)

Напряжение измеряется в вольтах (В), используются значения в киловольтах (кВ), милливольтах (мВ) и микровольтах (мкВ).

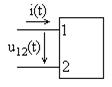Ток и напряжение характеризуются направлением, которое указывается стрелкой, как показано на рис. 1.1. Они задаются произвольно до начала расчетов. Желательно, чтобы ток и напряжение для одного элемента цепи имели бы одинаковые поло-

Рис. 1.1 жительные направления. Обозначения могут

иметь индексы, например, напряжение 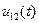между точками 1 и 2 на рис. 1.1.

Численные значения тока и напряжения характеризуются знаком. Если знак положительный, то это означает, что истинное положительное направление совпадает с заданным, а иначе они противоположны.

Движение зарядов в электрической цепи характеризуются энергией и мощностью. Для перемещения бесконечно малого заряда 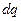между точками 1 и 2 с напряжением 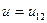в цепи на рис. 1.1 необходимо затратить бесконечно малую энергию 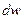, равную

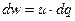, (1.4)

тогда энергия цепи в интервале времени от 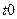до 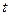с учетом (1.1) определяется выражением

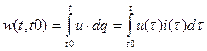. (1.5)

При постоянных токе 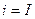и напряжении 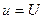энергия равна 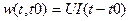и неограниченно растет с течением времени. Это относится и к общему выражению (1.5), что делает энергию цепи достаточно неудобной технической характеристикой.

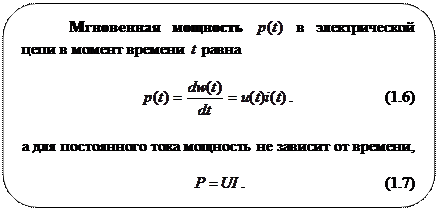
Мгновенная мощность 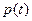зависит от времени и может быть положительной (цепь потребляет энергию извне) и отрицательной (цепь отдает ранее накопленную энергию).

Средняя мощность всегда неотрицательна, если внутри цепи отсутствуют источники электрической энергии.

Энергия измеряется в джоулях (Дж), а мгновенная и средняя мощности – в ваттах (Вт).

1.3. Элементы электрической цепи

Элемент – это неделимая часть электрической цепи. В физической цепи (радиоприемнике) имеются физические элементы (резисторы, конденсаторы, катушки индуктивности, диоды, транзисторы и т.д.). Они имеют сложные свойства и математический аппарат их точного описания на основе теории электромагнитного поля.

При расчете электрической цепи необходимо разработать достаточно точные, простые и удобные с инженерной точки зрения модели физических элементов, которые в дальнейшем будем называть элементами.

Инженерные модели в электротехнике строятся на основе физических представлений о взаимосвязи в них тока и напряжения. Свойства резистивных двухполюсных (с двумя выводами) элементов описываются вольтамперными характеристиками (ВАХ) – зависимостью тока через элемент от приложенного к нему напряжения 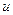. Эта зависимость может быть прямолинейной (для резистора на рис. 1.2а) или нелинейной (для полупроводникового диода на рис.1.2б).

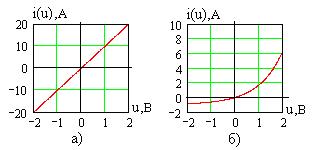
Рис. 1.2

Элементы с прямолинейной ВАХ называют линейными, а иначе – нелинейными. Аналогично рассматриваются емкостные элементы, для которых используют кулон – вольтную характеристику (зависимость накопленного заряда от приложенного напряжения), и индуктивные с использованием вебер - амперной характеристики (зависимости магнитного потока от протекающего через элемент тока).

1.4. Модели основных линейных элементов цепи

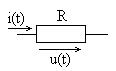
Основными линейными элементами электрической цепи являются резистор, конденсатор и катушка индуктивности. Их условно-графические обозначения показаны на рис. 1.3 (сверху указаны названия физических элементов, а внизу – их моделей).

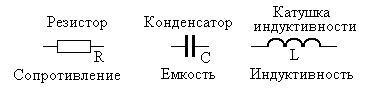
Рис. 1.3

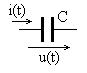Сопротивление (модель резистора) в соответствии с рис. 1.4 строится на основе закона Ома в классической формулировке,

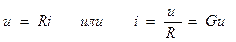, (1.10)

где - параметр модели, называемый сопротивлением, а 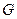- проводимостью,

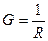. (1.11)

Рис. 1.4

Как видно из (1.10), сопротивление – это линейный элемент (с прямолинейной ВАХ). Его параметр - сопротивление - измеряется в Омах (Ом) или внесистемных единицах – килоомах (кОм), мегаомах (Мом) или гигаомах (ГОм). Проводимость 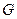определяется выражением (1.11), обратна сопротивлению и измеряется в 1/Ом. Сопротивление и проводимость элемента не зависят от величин тока и напряжения.

В сопротивлении ток и напряжение пропорциональны друг другу, имеют одинаковую форму.

Мгновенная мощность электрического тока в сопротивлении равна

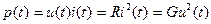. (1.12)

Как видно, мгновенная мощность в сопротивлении не может быть отрицательна, то есть сопротивление всегда потребляет мощность (энергию), преобразуя ее в тепло или другие виды, например, в электромагнитное излучение. Сопротивление – это модель диссипативного элемента, рассеивающего электрическую энергию.

Емкость (модель конденсатора) в соответствии с рис.1.5 формируется исходя из того, что накопленный в ней заряд пропорционален приложенному напряжению,

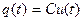. (1.13)

Параметр модели – емкость 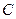- не зависит

Рис. 1.5 от тока и напряжения и измеряется в фарадах

(Ф). Величина емкости 1 Ф очень велика, на практике широко используются значения в микрофарадах (1 мкФ = 10^-6 Ф), нанофарадах (1 нФ = 10^-9 Ф) и пикофарадах (1 пФ = 10^-12 Ф).

Подставляя (1.13) в (1.1), получим модель для мгновенных значений тока и напряжения

.

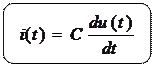(1.14)

Из (1.14) можно записать обратное выражение для модели,

.

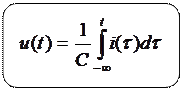(1.15)

Мгновенная электрическая мощность в емкости равна

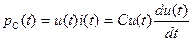. (1.16)

Если напряжение положительно и увеличивается с течением времени (его производная больше нуля), то мгновенная мощность положительна и емкость накапливает в себе энергию электрического поля. Аналогичный процесс имеет место, если напряжение отрицательно и продолжает уменьшаться.

Если же напряжение емкости положительно и падает (отрицательно и растет), то мгновенная мощность отрицательна, а емкость отдает во внешнюю цепь ранее накопленную энергию.

Таким образом, емкость – это элемент, накапливающий электрическую энергию (подобно банке, в которой накапливается вода, и из которой она может выливаться), потери энергии в емкости отсутствуют.

Накопленная в емкости энергия определяется выражением

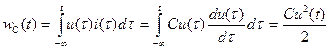. (1.17)

Индуктивность (модель катушки индуктивности) формируется исходя из того, что потокосцепление 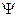, равное произведению магнитного потока 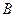(в веберах) на число витков катушки 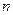, прямо пропорционально протекающему через нее току (рис. 1.6),

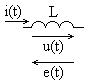
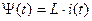, (1.18)

где 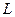- параметр модели, который называется индуктивностью и измеряется в генри (Гн).

Рис. 1.6 Величина 1 Гн – это очень большая ин-

дуктивность, поэтому используют внесистемные единицы: миллигенри (1 мГн = 10^-3 Гн), микрогенри (1 мкГн = 10^-6 Гн) и наногенри (1 нГн = 10^-9 Гн).

Изменение потокосцепления в индуктивности вызывает электродвижущую силу (ЭДС) самоиндукции 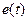, равную

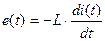(1.19)

и направленную противоположно току и напряжению, тогда 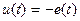и модель катушки индуктивности для мгновенных значений тока и напряжения принимает вид

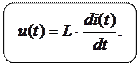. (1.20)

Можно записать обратное выражение модели,

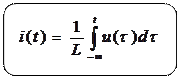(1.21)

Мгновенная электрическая мощность в индуктивности равна

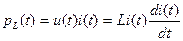. (1.22)

Если ток положителен и растет, или отрицателен и падает, то мгновенная мощность положительна и индуктивность накапливает в себе энергию магнитного поля. Если же ток индуктивности положителен и падает (отрицателен и растет), то мгновенная мощность отрицательна, и индуктивность отдает во внешнюю цепь ранее накопленную энергию.

Таким образом, индуктивность (как и емкость) – это элемент, только накапливающий энергию, потери энергии в индуктивности отсутствуют.

Накопленная в индуктивности энергия равна

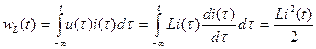. (1.23)

1.5. Законы Ома для элементов цепи

Рассмотренные модели элементов электрической цепи, определяющие взаимосвязь между мгновенными значениями токов и напряжений, будем в дальнейшем называть законами Ома для элементов цепи, хотя собственно закон Ома относится лишь к сопротивлению.

Эти соотношения сведены в табл. 1.1. Они являются линейными математическими операциями и относятся только к линейным элементам.

В нелинейных элементах связь между током и напряжением существенно сложнее и в целом может быть описана нелинейными интегро-дифференциальными уравнениями, для которых отсутствуют общие методы решения.

Таблица 1.1

Законы Ома в элементах цепи для мгновенных значений тока и напряжения

Элемент	Зависимость тока от напряжения	Зависимость напряжения от тока
R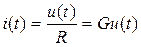
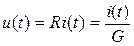
L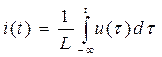
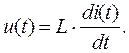
C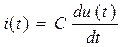

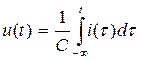
1.6. Расчет тока и напряжения в элементах цепи

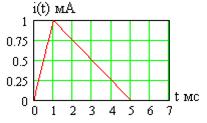В качестве примера проведем расчет напряжения на элементах цепи при заданной зависимости тока от времени, показанной на рис. 1.7.

Математически эту зависимость можно записать

Рис. 1.7 в виде

(1.24)

Необходимо помнить, что в (1.24) время 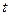измеряется в миллисекундах, а ток - миллиамперах.

Тогда в показанном на рис. 1.4. сопротивлении при 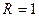кОм напряжение равно 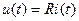(рис. 1.8а) и мощность 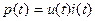(рис. 1.8б). Формы временных диаграмм тока и напряжения в сопротивлении совпадают, а произведение двух прямолинейных зависимостей и 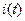дает параболические кривые изменения мощности .

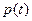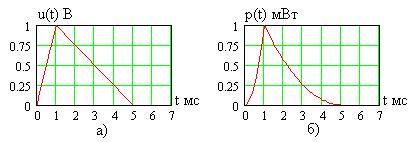
Рис. 1.8

В емкости (рис.1.5) 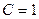мкФ мгновенные значения тока и напряжения связаны между собой выражениями (1.14) или (1.15). Для тока (рис.1.7) вида (1.24) из

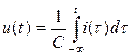(1.25)

получим формулу для напряжения на емкости в вольтах

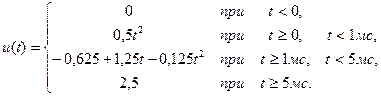(1.26)

Расчет при 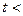1 мс выполняется очевидно. При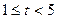

интеграл (1.25) записывается в виде

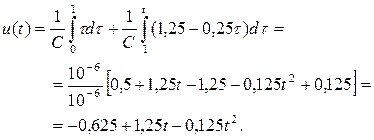(1.27)

На интервале времени 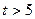мс интеграл (1.25) имеет вид

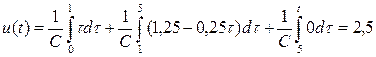(1.28)

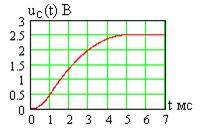и является константой. Временная диаграмма показана на рис. 1.9. Как видно, на интервале времени 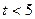мс, пока действует импульс тока, происходит заряд конденсатора, а затем напряжение заряженной емкости не меняется. На рис. 1.10а показана зависимость от времени мгновенной мощности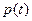

Рис. 1.9 (1.16), а на рис. 1.10б – накоп-

ленной в емкости энергии 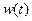(1.17). Как видно, емкость только накапливает энергию, так как разряд не происходит (ток вида рис. 1.7 принимает только положительные значения).

Для получения формулы мощности 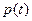необходимо перемножить выражения (1.24) и (1.26) на соответствующих

временных интервалах (получим полином третьей степени ).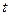

Энергия 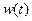определяется из (1.17) при подстановке (1.26), что приводит к полиномам четвертой степени .

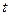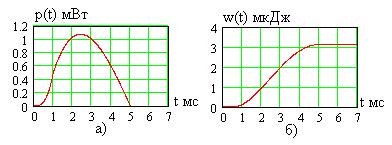
Рис. 1.10

Для индуктивности рис. 1.6 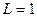Гн при токе, показанном на рис. 1.7 напряжение определяется выражением (1.20)

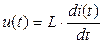, (1.29)

тогда при подстановке (1.24) для в вольтах получим

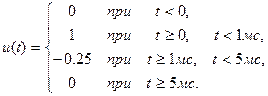(1.30)

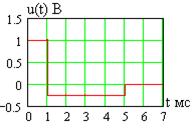
Эта зависимость показана на рис. 1.11. При графическом дифференцировании прямолинейных зависимостей на рис. 1.7 получим на соответствующих интервалах времени константы, что соответствует рис. 1.11.

Рис. 1.11

Мощность определяется выражением (1.22), тогда для 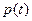в милливаттах получим

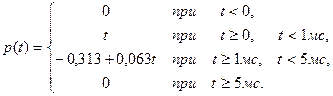(1.31)

Зависимость 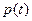показана на рис. 1.12а. Накопленная в индуктивности энергия вычисляется по формуле (1.23), тогда график 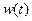имеет вид, показанный на рис. 1.12б.

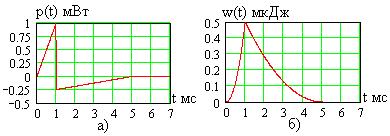
Рис. 1.12

Как видно, мгновенная мощность с ростом тока на интервале времени от 0 до 1мс прямо пропорционально увеличивается, а накопленная в индуктивности энергия растет по квадратичному закону. Когда ток начинает падать при 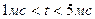, то напряжение и мощность 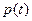становятся отрицательными (рис. 1.11 и рис. 1.12а), а это означат, что индуктивность отдает ранее накопленную энергию, которая начинает снижаться по квадратичному закону (рис. 1.12б).

Расчет сигналов и энергетических характеристик в элементах цепи R, L и C можно провести с помощью программы MathCAD.

1.7. Идеальные источники сигнала

Электрические сигналы (токи и напряжения) возникают в цепи при воздействии на нее источников. Физические источники – это батареи и аккумуляторы, формирующие постоянные ток и напряжение, генераторы переменных напряжений различной формы и другие электронные устройства. На их зажимах (полюсах) возникает напряжение (разность потенциалов) и через них протекает ток за счет электрохимических процессов или других сложных физических явлений. В физике их обобщенное действие характеризуют электродвижущей силой (ЭДС).

Для расчета электрических цепей необходимы модели источников сигнала. Простейшими из них являются идеальные источники.

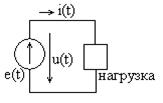Графическое изображение (обозначение) идеального источника напряжения показано на рис. 1.13 в виде окружности со стрелкой, указывающей положительное направление ЭДС 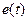. На полюсах источника возникает напряжение , которое при указанных положительных направлениях равно ЭДС,

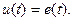(1.32)

Рис. 1.13

Если изменить положительное

направление ЭДС или напряжения (сделать их встречными), в формуле появится знак минус.

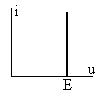
К источнику подключается нагрузка и тогда через нее протекает ток 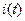. Свойства источника постоянного напряжения или тока описываются его вольтамперной характеристикой (ВАХ) – зависимостью тока от напряжения 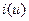. Идеальный источник напряжения с ЭДС, равной 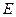имеет вольтамперную характеристику, показанную на рис. 1.14. Если рассматривается источник переменного сигнала, то от тока не зависят все его пара-

Рис. 1.14 метры.

Как видно, с ростом тока при постоянном напряжении мощность, отдаваемая идеальным источником напряжения в нагрузку, стремится к бесконечности. Это является следствием выбранной идеальной модели (формы ВАХ) и ее недостатком, так как любой физический источник не может отдать бесконечную мощность.

Графическое изображение идеального источника тока 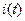показано на рис. 1.15а в виде окружности, внутри которой указано положительное направление тока. При подключении нагрузки на полюсах источника возникает напряжение с указанным положительным направлением.

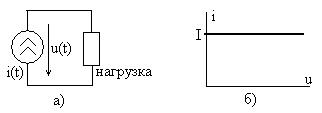
Рис. 1.15

Дата добавления: 2014-11-25