
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследование функций
|
|
|
|
Функция 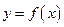 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке  , если для любых
, если для любых  ,
, 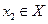 ,
, 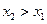 верно неравенство
верно неравенство 
 .
.
Если производная дифференцируемой функции положительна внутри некоторого промежутка  , то она возрастает на этом промежутке.
, то она возрастает на этом промежутке.
Если производная дифференцируемой функции отрицательна внутри некоторого промежутка  , то она убывает на этом промежутке.
, то она убывает на этом промежутке.
Точка 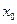 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 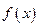 , если для всех
, если для всех 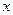 из некоторой окрестности точки
из некоторой окрестности точки 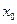 выполняется неравенство
выполняется неравенство 
 .
.
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимумы и минимумы функции называются экстремумами функции.
Для того чтобы дифференцируемая функция 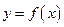 имела в точке
имела в точке 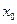 экстремум, необходимо, чтобы
экстремум, необходимо, чтобы 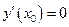 и достаточно, чтобы при переходе через точку
и достаточно, чтобы при переходе через точку 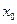 происходила смена знака первой производной.
происходила смена знака первой производной.
Пример 9.1. Найти экстремумы функции  .
.
Решение.
1. Дифференцируя данную функцию, находим 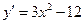 .
.
2. Приравнивая производную к нулю, находим критические точки функции 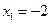 ,
, 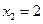 . Точек, в которых производная не существует, у данной функции нет –
. Точек, в которых производная не существует, у данной функции нет – 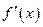 определена на всей числовой оси.
определена на всей числовой оси.
3. Нанесем критические точки на числовую прямую и определим знак производной на каждом интервале.
 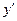
| + | – | + | |
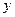
| -2 | 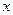
|
Согласно достаточному условию точка 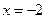 является точкой максимума, точка
является точкой максимума, точка 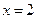 – точкой минимума.
– точкой минимума.
4. Находим 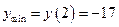 ,
,  .
.
График функции 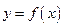 называетсявыпуклым (вогнутым) на интервале
называетсявыпуклым (вогнутым) на интервале  , если он расположен ниже (выше) любой касательной к графику функции на этом интервале.
, если он расположен ниже (выше) любой касательной к графику функции на этом интервале.
Достаточное условие существования точки перегиба. Пусть график функции определяется уравнением 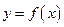 . Если
. Если 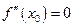 или не существует, и при переходе через значение
или не существует, и при переходе через значение  вторая производная
вторая производная  меняет знак, то точка
меняет знак, то точка  есть точка перегиба.
есть точка перегиба.
Пример 9.2. Исследовать на выпуклость, вогнутость и точки перегиба график функции 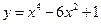
Решение.
1. Дифференцируя данную функцию дважды, находим  ,
, 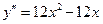 .
.
2. Приравнивая вторую производную к нулю, и находим точки, в которых вторая производная равна нулю  ,
,  .
.
3. Нанесем точки на числовую прямую и определим знак второй производной на каждом интервале.
 
| + | – | + | |
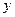
| -1 | 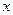
|
4. Функция выпукла вниз на интервалах  ,
,  , вверх –
, вверх –  . Точки
. Точки  ,
,  являются точками перегиба.
являются точками перегиба.
Асимптотой графика функции 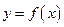 называется прямая, расстояние до которой от точки, лежащей на графике функции, стремится к нулю при неограниченном удалении этой точки от начала координат вдоль графика.
называется прямая, расстояние до которой от точки, лежащей на графике функции, стремится к нулю при неограниченном удалении этой точки от начала координат вдоль графика.
Для нахождения асимптот пользуются следующими положениями:
1. Пусть функция 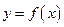 определена в некоторой окрестности точки
определена в некоторой окрестности точки 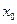 (исключая, возможно, саму эту точку) и хотя бы один из пределов функции
(исключая, возможно, саму эту точку) и хотя бы один из пределов функции  (слева) или при
(слева) или при  (справа) равен бесконечности, т.е.
(справа) равен бесконечности, т.е.  или
или 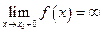 . Тогда прямая
. Тогда прямая  является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 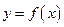 .
.
2. Пусть функция 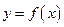 определена при достаточно больших
определена при достаточно больших 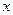 и существует конечный предел функции
и существует конечный предел функции 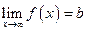 . Тогда прямая
. Тогда прямая  есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 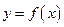 .
.
3. Пусть функция 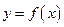 определена при достаточно больших
определена при достаточно больших 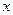 и существует конечные пределы
и существует конечные пределы  и
и 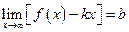 . Тогда прямая
. Тогда прямая 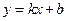 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 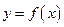 .
.
Пример. 9.3. Найти вертикальные асимптоты графика функции  .
.
Решение. Точка  – точка разрыва II рода. Так как
– точка разрыва II рода. Так как 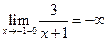 ,
, 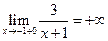 , то прямая
, то прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
Пример 9.4. Найти горизонтальные асимптоты графика функции 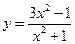 .
.
Решение. Так как 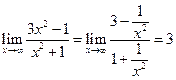 , то прямая
, то прямая  является горизонтальной асимптотой.
является горизонтальной асимптотой.
Пример 9.5. Найти наклонные асимптоты графика функции  .
.
Решение. Так как  ,
, 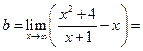
 , то прямая
, то прямая  является наклонной асимптотой.
является наклонной асимптотой.
При исследовании функций и построении их графиков рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
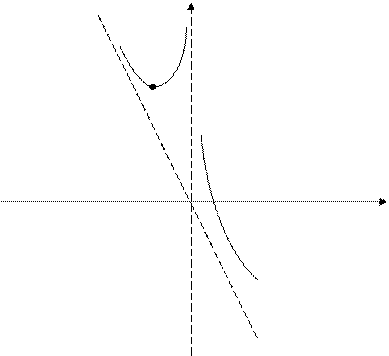
Пример 9.6. Исследовать функцию  и построить ее график.
и построить ее график.
Решение.
1. Область определения функции:  .
.
2. Функция общего вида, так как 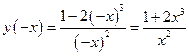 .
.
3. Вертикальные асимптоты могут пересекать ось абсцисс в точке  . Так как
. Так как 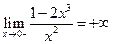 ,
,  , то прямая
, то прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
4. Поведение функции в бесконечности. Вычислим:  . Функция горизонтальных асимптот не имеет.
. Функция горизонтальных асимптот не имеет.
Так как  ,
, 
 , то прямая
, то прямая 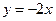 является наклонной асимптотой.
является наклонной асимптотой.
5. Найдем экстремумы и интервалы монотонности функции. Дифференцируя данную функцию, находим 
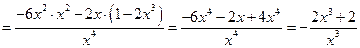 . Приравнивая производную к нулю, находим критические точки функции
. Приравнивая производную к нулю, находим критические точки функции  . В точке
. В точке  производная не существует. Определим знак производной на каждом интервале.
производная не существует. Определим знак производной на каждом интервале.
 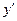
| – | + | – | |
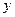
| -1 | 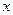
|
Функция возрастает на интервале 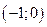 , убывает –
, убывает –  ,
,  . Точка
. Точка  является точкой минимума
является точкой минимума 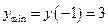 .
.
6. Определим интервалы выпуклости функции и точки перегиба.
Найдем производную второго порядка 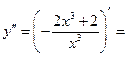
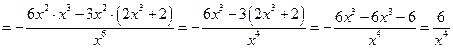 . Приравнивая вторую производную к нулю, и находим точки, в которых вторая производная равна нулю или не существует
. Приравнивая вторую производную к нулю, и находим точки, в которых вторая производная равна нулю или не существует 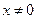 . Знаки производной второго порядка указаны на рисунке.
. Знаки производной второго порядка указаны на рисунке.
 
| + | + | |
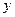
| 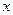
|
Функция выпукла вверх на интервалах  ,
, 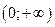 . Точек перегиба нет.
. Точек перегиба нет.
7. Точка  является точкой пересечения функции с осью абсцисс.
является точкой пересечения функции с осью абсцисс.
 |
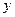
| |||||||||
| -4 | -3 | -2 | -1 | 
| |||||
| -1 | |||||||||
| -2 | |||||||||
| -3 |
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 442; Нарушение авторских прав?; Мы поможем в написании вашей работы!