
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы векторной алгебры
|
|
|
|
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь длина, объем, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называются векторными. Векторная величина геометрически изображается с помощью вектора.
Вектором называется направленный отрезок 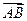 с начальной точкой
с начальной точкой  и конечной точкой
и конечной точкой 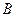 .
.
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, т.е. 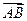 ,
,  .
.
Длиной (или модулем) вектора 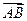 называется длина отрезка, изображающего вектор и обозначается
называется длина отрезка, изображающего вектор и обозначается 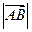 .
.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 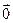 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается через 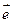 .
.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Сложение векторов. Пусть  и
и  – два произвольных вектора, рис. 5.1а. Возьмем произвольную точку
– два произвольных вектора, рис. 5.1а. Возьмем произвольную точку 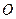 и построим вектор
и построим вектор 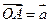 . От точки
. От точки  отложим вектор
отложим вектор 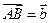 . Вектор
. Вектор 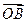 , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
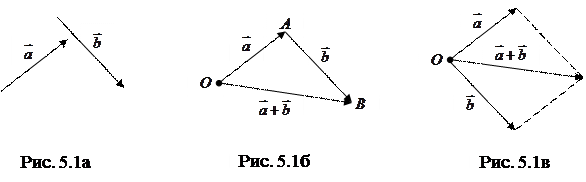
и  , рис. 5.1б. Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма, рис. 5.1в.
, рис. 5.1б. Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма, рис. 5.1в.
 |
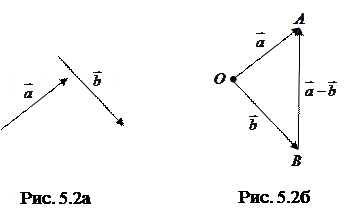
Вычитание векторов. Пусть  и
и  – два произвольных вектора, рис. 5.2а. Возьмем произвольную точку
– два произвольных вектора, рис. 5.2а. Возьмем произвольную точку 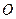 и построим вектор
и построим вектор 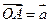 и
и 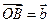 . Вектор
. Вектор 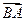 , соединяющий конец второго вектора с концом первого, называется разностью векторов
, соединяющий конец второго вектора с концом первого, называется разностью векторов  и
и  , рис. 5.2б.
, рис. 5.2б.
 |
Умножение вектора на число. Произведением вектора на скаляр (число) 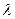 называется вектор
называется вектор 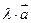 , имеющий длину
, имеющий длину 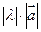 , коллинеарный вектору
, коллинеарный вектору  и направленный в туже сторону, что и вектор
и направленный в туже сторону, что и вектор  , если
, если 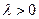 , и в противоположную сторону, если
, и в противоположную сторону, если 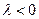 .
.
Пример 5.1. Даны три вектора 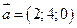 ,
, 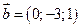 ,
, 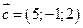 . Найти координаты вектора
. Найти координаты вектора 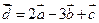 .
.
Решение. Так как при умножении вектора на число его координаты умножаются на это число, то 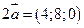 ,
, 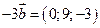 . При сложении векторов их соответствующие координаты складываются, следовательно,
. При сложении векторов их соответствующие координаты складываются, следовательно, 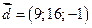 .
.
Зная координаты вектора можно определить его длину. Длина вектора 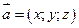 вычисляется по формуле
вычисляется по формуле 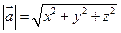 .
.
Пример 5.2. Даны точки 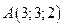 и
и 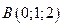 . Найти длину вектора
. Найти длину вектора 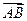 .
.
Решение. Найдем координаты вектора 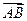 :
: 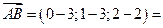
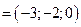 . Длина вектора
. Длина вектора 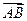 равна
равна  .
.
Скалярным произведением 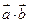 двух векторов
двух векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.
называется число, равное произведению длин этих векторов на косинус угла между ними, т.е. 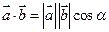 .
.
Пример 5.3. Найти скалярное произведение векторов  и
и  , если
, если 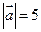 ,
, 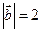 ,
, 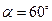 .
.
Решение. Так как 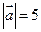 ,
, 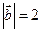 ,
, 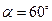 , то скалярное произведение векторов
, то скалярное произведение векторов  и
и  равно
равно 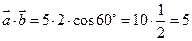 .
.
Скалярное произведение векторов можно выразить через координаты векторов 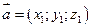 и
и 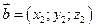 :
: 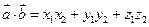 , тогда угол между векторами
, тогда угол между векторами  и
и  определяется по формуле
определяется по формуле 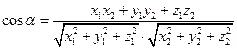 .
.
Пример 5.4. Найти скалярное произведение векторов  и
и  , и угол между ними, если
, и угол между ними, если 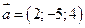 ,
, 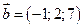 .
.
Решение. Скалярное произведение векторов  и
и  равно
равно 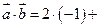
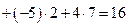 .
.
Длина вектора  равна
равна  , длина вектора
, длина вектора  –
– 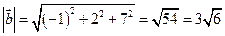 . Косинус угла между векторами
. Косинус угла между векторами  и
и  равен
равен 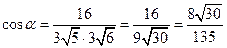 , откуда
, откуда 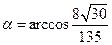 .
.
Векторы  ,
,  и
и 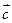 называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Три некомпланарных вектора  ,
,  и
и 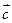 , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора  кратчайший поворот от первого вектора
кратчайший поворот от первого вектора  ко второму вектору
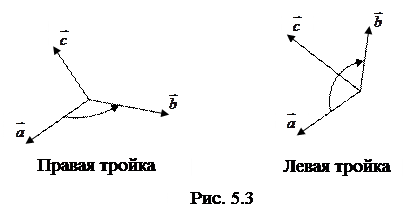
ко второму вектору  виден совершающимся против часовой стрелки, и левую, если по часовой, рис. 5.3.
виден совершающимся против часовой стрелки, и левую, если по часовой, рис. 5.3.
 |
Векторным произведением вектора  на вектор
на вектор  называют такой вектор
называют такой вектор  , который определяется тремя условиями:
, который определяется тремя условиями:
1. длина вектора  равна
равна 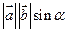 где
где 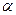 угол между векторами
угол между векторами  и
и  ;
;
2. вектор 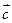 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и  ;
;
3. векторы  ,
,  и
и 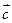 образуют правую тройку векторов.
образуют правую тройку векторов.
Векторное произведение  на
на  обозначается
обозначается 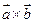 .
.
Если векторы  и
и  заданы своими координатами в декартовой системе координат:
заданы своими координатами в декартовой системе координат: 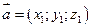 ,
, 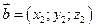 , то векторное произведение
, то векторное произведение 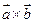 можно найти с помощью разложения определителя:
можно найти с помощью разложения определителя: 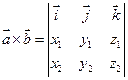 .
.
Пример 5.5. Найти векторное произведение векторов  и
и  , если
, если 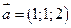 ,
, 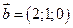 .
.
Решение. Векторное произведение векторов  и
и  равно
равно 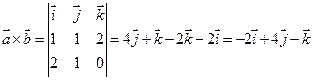 или
или 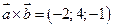 .
.
Согласно определению векторного произведения векторов  и
и 
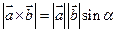 , тогда площадь параллелограмма, построенного на векторах
, тогда площадь параллелограмма, построенного на векторах  и
и  равна модулю векторного произведения этих векторов, т.е.
равна модулю векторного произведения этих векторов, т.е. 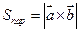 , а площадь треугольника
, а площадь треугольника 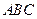 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах  и
и  , т.е.
, т.е. 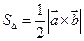 .
.
Пример. 5.6. Вычислить площадь параллелограмма, построенного на векторах  ,
,  .
.
Решение. Векторное произведение векторов  и
и  равно
равно 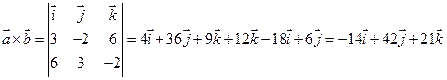 или
или 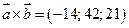 . Площадь параллелограмма, построенного на векторах
. Площадь параллелограмма, построенного на векторах  ,
,  равна
равна 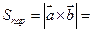
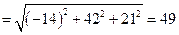 кв. ед.
кв. ед.
Смешанными произведением векторов трех векторов  ,
,  и
и 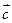 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на векторное произведение векторов
на векторное произведение векторов  и
и 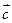 , т.е.
, т.е. 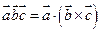 .
.
Если векторы  ,
,  и
и 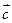 заданы своими координатами в декартовой системе координат:
заданы своими координатами в декартовой системе координат: 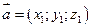 ,
, 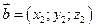 ,
, 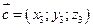 , то смешанное произведение
, то смешанное произведение 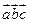 можно найти по формуле:
можно найти по формуле: 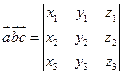 .
.
Пример 5.7. Найти смешанное произведение 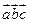 , если
, если 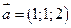 ,
, 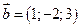 ,
, 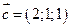 .
.
Решение. Смешанное произведение векторов равно 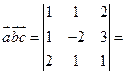
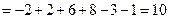 .
.
Смешанное произведение трех векторов  ,
,  и
и 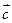 равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку, т.е.
равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку, т.е. 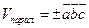 . Объем тетраэдра, построенного на этих же векторах, равен
. Объем тетраэдра, построенного на этих же векторах, равен 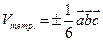 .
.
Пример 5.8. Найти объем тетраэдра с вершинами в точках 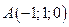 ,
, 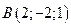 ,
, 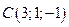 ,
, 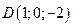 .
.
Решение. Найдем координаты векторов 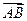 ,
, 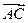 ,
, 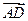 :
: 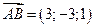 ,
,  ,
, 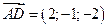 . Искомый объем тетраэдра равен
. Искомый объем тетраэдра равен 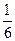 объема параллелепипеда, построенного на векторах
объема параллелепипеда, построенного на векторах 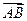 ,
, 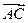 ,
, 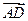 . Таким образом,
. Таким образом, 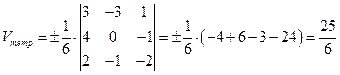 куб. ед.
куб. ед.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1069; Нарушение авторских прав?; Мы поможем в написании вашей работы!