
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители квадратных матриц
|
|
|
|
Определитель (детерминант) – это число, соответствующее данной квадратной матрице и вычисленное по определенному правилу.
Для обозначения определителей используются следующие символы:  ,
, 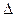 ,
, 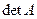 . Символ
. Символ  обозначает таблицу (матрицу), для которой вычисляется определитель.
обозначает таблицу (матрицу), для которой вычисляется определитель.
Определитель матрицы первого порядка  или просто определитель первого порядка равен самому числу
или просто определитель первого порядка равен самому числу 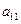 :
: 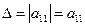 .
.
Например, пусть 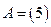 , тогда
, тогда 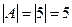 .
.
Определителем матрицы второго порядка 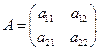 , или определителем второго порядка называется число, которое вычисляется по формуле:
, или определителем второго порядка называется число, которое вычисляется по формуле: 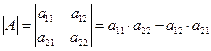 .
.
Например, пусть 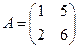 , тогда
, тогда  .
.
Определителем матрицы третьего порядка 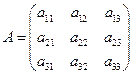 или определителем третьего порядка называется число, которое вычисляется по формуле:
или определителем третьего порядка называется число, которое вычисляется по формуле:  .
.
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы.
Вычисление определителя третьего порядка иллюстрируется схемой:


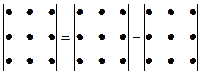 .
.
Пример 2.1. Вычислить определители третьего порядка 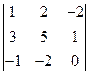 .
.
Решение. 
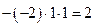 .
.
Минором 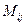 элемента
элемента 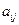 матрицы
матрицы 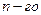 порядка называется определитель матрицы
порядка называется определитель матрицы 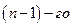 порядка, полученной из матрицы
порядка, полученной из матрицы  вычеркиванием
вычеркиванием  строки и
строки и 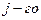 столбца.
столбца.
Пример 2.2. Найти минор элемента  матрицы третьего порядка
матрицы третьего порядка 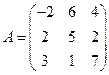 .
.
Решение. Из полученной матрицы  вычеркнем первую строку, и третий столбец, получим
вычеркнем первую строку, и третий столбец, получим 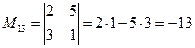 .
.
Алгебраическим дополнением 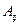 элемента
элемента 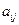 матрицы
матрицы 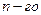 порядка называется его минор, взятый со знаком
порядка называется его минор, взятый со знаком 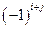 :
: 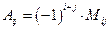 .
.
Пример 2.3. Найти алгебраическое дополнение элемента  матрицы третьего порядка
матрицы третьего порядка  .
.
Решение. Из полученной матрицы  вычеркнем первую строку, и второй столбец, полученный минор возьмем со знаком
вычеркнем первую строку, и второй столбец, полученный минор возьмем со знаком  , т.е.
, т.е.  .
.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 445; Нарушение авторских прав?; Мы поможем в написании вашей работы!