Матрицы и операции над ними

Рекомендации по решению типовых задач по алгебре и геометрии

Мурманск

На 2013 – 2014 учебный год

Контрольных работ по дисциплине

Методические рекомендации по выполнению

МУРМАНСКИЙ ФИЛИАЛ

МЧС РОССИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ
ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ МЧС РОССИИ

«ВЫСШАЯ МАТЕМАТИКА»

для студентов заочной формы обучения

по специальностям: 280705.65 «Пожарная безопасность»

(форма отчетности – экзамен)

280700.62 «Техносферная безопасность»

(форма отчетности – зачет)

ОГЛАВЛЕНИЕ

Рекомендации по решению типовых задач по алгебре и геометрии. 4

Рекомендации по решению типовых задач по дифференциальному исчислению 21

Рекомендации по решению типовых задач по интегральному исчислению.. 32

Рекомендуемая литература. 41

Матрицей размера называется прямоугольная таблица чисел, содержащая строк и столбцов.

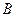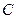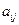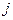Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например , , , …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: , где – номер строки, – номер столбца. Матрица записывается в виде

.

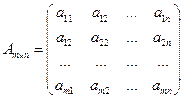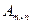Символ «» характеризует размер матрицы и обозначает ее порядок (размерность). Заметим, что матрицы и 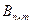есть матрицы разного порядка.

Виды матриц:

1. Матрица–строка – матрица, состоящая из одной строки. Например, – матрица–строка.

2. Матрица–столбец – матрица, состоящая из одного столбца. Например, 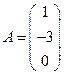– матрица–столбец.

3. Квадратная матрица – матрица, у которой число строк равно числу столбцов. Например, 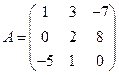– квадратная матрица третьего порядка.

4. Диагональная матрица – квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю. Например, 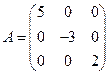– диагональная матрица третьего порядка.

5. Единичная матрица – диагональная матрица, у которой каждый элемент главной диагонали равен единице. Например, – единичная матрица четвертого порядка.

6. Нулевая матрица – матрица, все элементы которой равны нулю. Например, 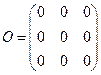– нулевая матрица третьего порядка.

7. Транспонированная матрица – матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером. Например, для матрицы 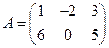, транспонированная матрица имеет вид .

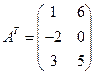Над матрицами, как и над числами можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые – специфические.

Умножение матрицы на число. Произведением матрицы на число 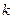называется матрица , элементы которой , (, ).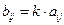

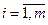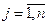Пример 1.1. Умножить матрицу 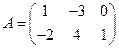на число 4.

Решение. .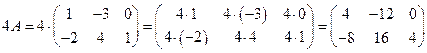

Сложение матриц. Суммой двух матриц и 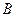одинакового размера называется матрица 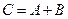, элементы которой , (, ).

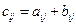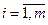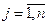Пример 1.2. Пусть , 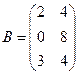. Найти .

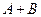Решение. .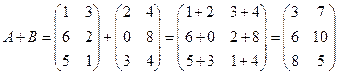

Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: .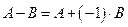

Умножение матриц. Произведение матриц имеет место только для матриц определенных размерностей. Матрицу можно умножить на матрицу 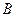, если число столбцов матрицы равно числу строк матрицы 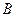, т.е. если имеет размерность , то матрица 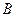должна иметь размерность 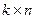. Произведением будет матрица размерности .

Произведением матриц называется матрица , каждый элемент которой равен сумме произведений элементов 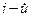строки матрицы на соответствующие элементы 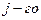столбца матрицы .

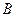Пример 1.3. Вычислить произведение матриц 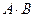, где , .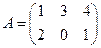

Решение. Найдем размер матрицы-произведения: 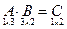. Вычислим элементы матрицы-произведения 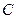, умножая элементы строки матрицы на соответствующие элементы столбцов матрицы : .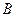

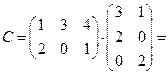
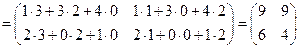Пример 1.4. Найти матрицу 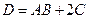, если , , .

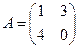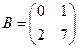Решение. Произведение матриц и 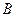возможно. Умножая элементы строки матрицы на соответствующие элементы столбцов матрицы 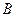, получим .

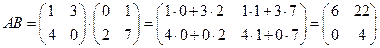Умножим матрицу 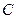на число 2, получим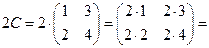

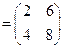. Найдем сумму матриц 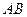и :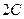

.

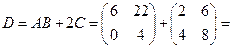
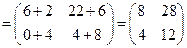Дата добавления: 2014-11-25