Элементы аналитической геометрии

Линия на плоскости часто задается множеством точек, обладающих некоторым только присущим геометрическим свойством. Например, окружность радиуса 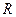есть множество всех точек плоскости, удаленных на расстоянии 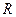от некоторой фиксированной точки 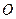(центра окружности).

Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел – ее координат, а положение линии на плоскости определять с помощью уравнения (т.е. равенства связывающее координаты точки линии).

Уравнение линии (или кривой) на плоскости 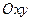называется такое уравнение 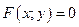с двумя переменными, которому удовлетворяют координаты 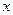и 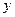каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Уравнение линии позволяет изучить ее геометрические свойства с помощью исследования ее уравнения. Простейшим из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.

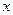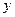Уравнение первой степени относительно и вида 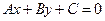называется общим уравнением прямой на плоскости, где , 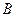и 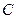– произвольные числа, причем и 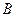не равны нулю одновременно.

Если в общем уравнении прямой 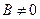, то, разрешив его относительно 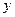, получим уравнение вида 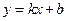, где 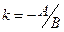, 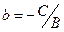. Его называют уравнением прямой с угловым коэффициентом, поскольку 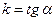, 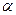– угол, образованный прямой с положительным направлением оси 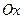. Свободный член уравнения 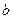равен ординате точки пересечения прямой с осью .

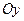Острый угол между двумя прямым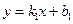и и 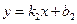определяется по формуле .

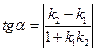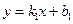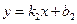Если прямые и параллельны, то условие параллельности имеет вид 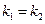. Если прямые перпендикулярны, то условие перпендикулярности имеет вид .

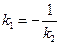Уравнение прямой, имеющей угловой коэффициент 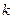и проходящей через точку 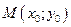записывается в виде .

Если известны координаты точек 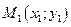и 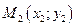, то уравнение прямой, проходящей через две точки имеет вид .

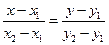Под расстоянием от точки 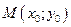до прямой 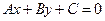понимается длина перпендикуляра, опущенного из точки на данную прямую. Расстояние от точки до прямой находится по формуле .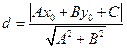

Пример 6.1. Составить уравнение прямой, проходящей через точк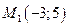и и .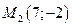

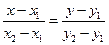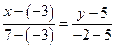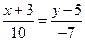Решение. Воспользуемся уравнением : или , откуда .

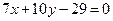Пример 6.2. Составить уравнение прямой, проходящей через точку параллельно прямой .

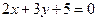Решение. Угловой коэффициент данной прямой равен 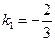. Искомая прямая параллельна данной, поэтому ее угловой коэффициент равен .

Используя уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом, получим уравнение искомой прямо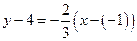й: или 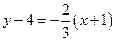, откуда .

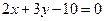Пример 6.3. Составить уравнение прямой, проходящей через точку 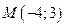перпендикулярно прямой .

Решение. Угловой коэффициент данной прямой равен 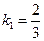. Искомая прямая перпендикулярна данной, поэтому ее угловой коэффициент равен .

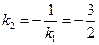Используя уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом, получим уравнение искомой прямо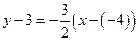й: или 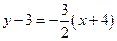, откуда .

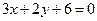Пример 6.4. Даны координаты точек 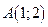, , 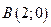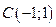. Найти:

1. уравнения сторон треугольника ;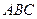

2. уравнение медианы, опущенной из вершины ;

3. длину и уравнение высоты, опущенной из вершины .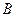

Решение.

1. Для нахождения уравнений сторон треугольника 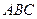воспользуемся формулой .

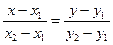Найдем уравнение стороны 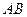: 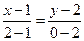, , 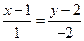, , 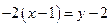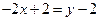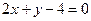. Найдем уравнение стороны 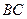: 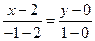, , 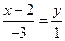, 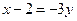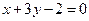. Найдем уравнение стороны : , , , , .

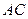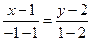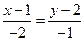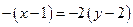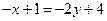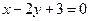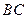2. Пусть точка середина стороны , тогда координаты точки равны 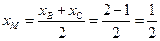, 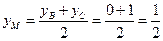. Уравнение медианы 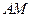определим по формуле 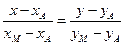. Найдем уравнение медианы 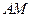: 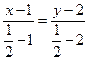, откуда .

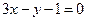3. Найдем уравнение прямой, проходящей через точку 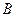перпендикулярно прямой .

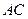Разрешив уравнение прямой 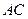относительно 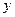, получим 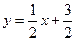. Угловой коэффициент прямой 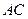равен 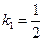. Искомая прямая перпендикулярна прямой 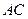, поэтому ее угловой коэффициент равен .

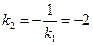Используя уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом, получим уравнение искомой прямой: 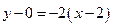, откуда .

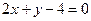Расстояние от точки 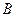до прямой 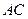равно .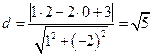

Уравнение плоскости, записанное в виде 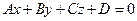, называется общим уравнением плоскости, где , , 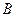, 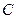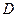– произвольные числа, причем , 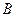и 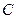не равны нулю одновременно, причем .

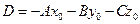Три точки пространства 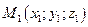, , 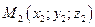, 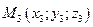не лежащие на одной прямой, определяют единственную плоскость. Уравнение 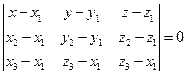есть уравнение плоскости, проходящей через три данные точки.

Пример 6.5. Написать уравнение плоскости, проходящей через точк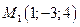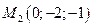и , и .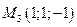

Решение. Воспользуемся формулой 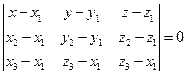. Так как 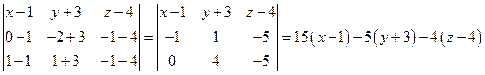. Запишем искомое уравнение плоскости .

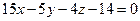Пусть даны уравнения двух плоскосте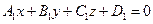й и .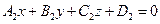

Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных 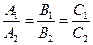, а условием их перпендикулярности .

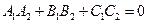Острый угол между плоскостями определяется по формуле .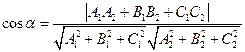

Пример 6.6. Найти острый угол между плоскостям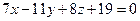и и .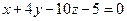

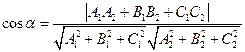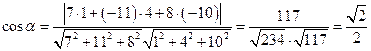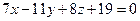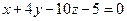Решение. Воспользуемся формулой . Так как , то угол между плоскостями и равен .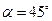

Пример 6.7. Даны координаты вершин треугольной пирамиды 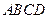: 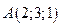, , 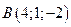, 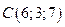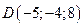. Требуется найти: длину ребра 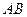; уравнение плоскости 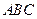; площадь грани 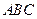; объем пирамиды.

Решение. Так как 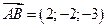, то длина ребр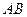а равна .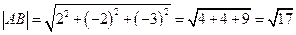

Найдем уравнение плоскости, проходящей через точки 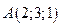, , 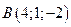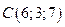: 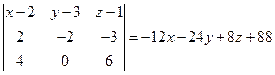. Уравнение плоскости 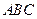имеет вид .

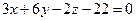Определим площадь грани 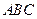. Координаты векторов равны 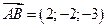, , 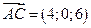векторное произведение равно 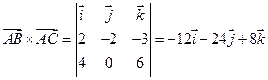. Площадь грани равна 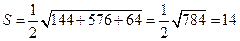кв. ед.

Объем треугольной пирамиды равен 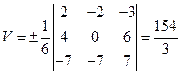куб. ед.

Дата добавления: 2014-11-25