Несобственные интегралы

Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур.

1. Пусть функция 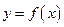неотрицательна и непрерывна на отрезке 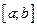. Тогда по геометрическому смыслу определенного интеграла площадь кривленной трапеции, расположенной «выше» оси абсцисс 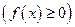на 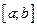(см. рис. 12.1), равна соответствующему определенному интегралу: .

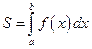2. Пусть функция 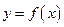неположительна и непрерывна на отрезке 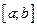. Тогда площадь кривленной трапеции, расположенной «ниже» оси абсцисс 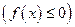на 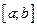(см. рис. 12.2 может быть найдена по формуле: .

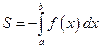3. Пусть на отрезке 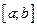задана непрерывная функция 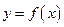общего вида. Предположим, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция 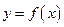будет знакопостоянна или равна нулю. Рассмотрим случай функции, изображенной на рис. 12.3 Площадь кривленной трапеции, равна алгебраической сумме соответствующих определенных интегралов: .

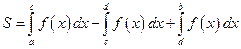4. Пусть на отрезке 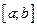заданы непрерывные функци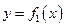и и 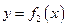, такие, что 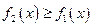. Тогда площадь 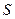фигуры, заключенной между кривым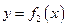и и 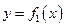, на отрезке 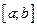вычисляется по формуле .

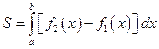Пример 12.1. Вычислить площади фигуры, ограниченных следующими линиями:

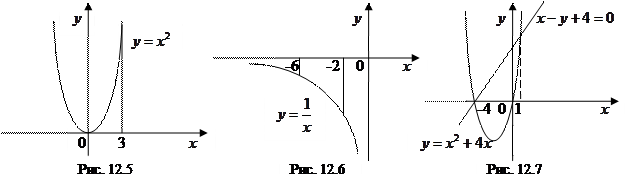
1. параболой 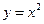, прямыми , 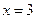и осью абсцисс;

2. гиперболой 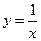, прямыми , 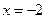и осью абсцисс;

3. параболой 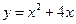и прямой .

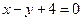Решение.

1. Из чертежа (см. рис. 12.5) видно, что искомая площадь кривленной трапеции расположенной «выше» оси абсцисс на отрезке 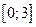, равна 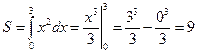кв. ед.

2. Искомая площадь кривленной трапеции расположенной «ниже» оси абсцисс на отрезке 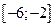, равна 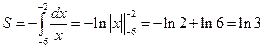кв. ед.

3. Найдем координаты точек пересечения параболы 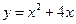и прямой 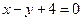, решив систему этих уравнений: 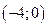, 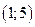. Воспользуемся формулой 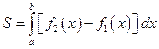, полагая 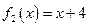, 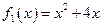. Абсциссы точек 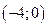, 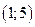пересечения наших линий зададут пределы интегрирования: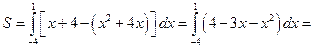 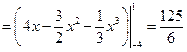кв. ед.

Вычисление объемов.

Объем тела, образованного вращением вокруг оси 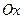криволинейной трапеции ограниченной непрерывной кривой 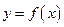, осью абсцисс и двумя прямым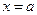и и 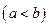находиться по формуле .

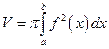Пример 12.2. Вычислить объем тела, образованного вращением вокруг оси 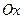криволинейной трапеции ограниченной непрерывной кривой 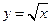и отрезком .

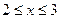Решение. Объем тела, образованного вращением вокруг оси 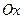криволинейной трапеции ограниченной непрерывной кривой 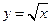и отрезком 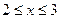равен 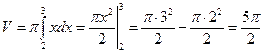куб. ед.

Пусть функция 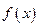определена на промежутке 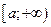и интегрируема по любому отрезку 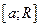, т.е. существует определённый интеграл 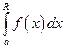при любом 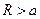. Тогда, если существует конечный предел 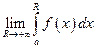, то его называют несобственным интегралом первого рода. Таким образом, по определению, .

В этом случае говорят, что несобственный интеграл существует или сходится. Если же вышеуказанный предел не существует или бесконечен, то говорят, что несобственный интеграл не существует или расходится.

Несобственный интеграл с двумя бесконечными пределами определяется как сумма интегралов: 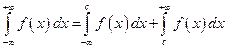, где 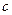– любое число, при условии существования обоих интегралов справа.

Пример 13.1. Вычислить несобственный интеграл .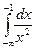

Решение. Найдем 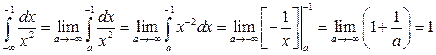, т.е. несобственный интеграл сходится.

Рекомендуемая литература

Основная:

1. Баврин И.И. Высшая математика: Учебник для вузов. – М.: «Академия», 2008. (Рекомендовано Министерством образования Российской Федерации в качестве учебника для студентов высших учебных заведений).

2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учебное пособие для втузов. Т. 1 / Н.С. Пискунов. – изд., стер. – М.: «Интеграл Пресс», 2007. – 416 с. (Допущено Министерством образования Российской Федерации в качестве учебного пособия для студентов Вуза).

3. Шипачёв В.С. Высшая математика: Учебник для вузов. – 5 изд., стер. – М.: Высшая школа, 2002. – 479 с. (Рекомендовано Министерством образования Российской Федерации в качестве учебника для студентов высших учебных заведений).

Дополнительная:

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры: Учебник для вузов. – 5-е изд. – М.: Наука, 1998. – 320 с.

2. Беклемишева Л.А. Сборник задач по аналитической геометрии и линейной алгебре: Учебное пособие /Л.А. Беклемишева, А.Ю. Петрович и др – М.: Наука, 1997. – 496 с.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учебное пособие. – СПб: Профессия, 2007. – 432 с.

4. Запорожец Г.И. Руководство к решению задач по математическому анализу: Учебное пособие. /Г.И. Запорожец – 4-е изд. – М.: Высшая школа, 1998. – 460 с.

5. Кудрявцев А.В. Краткий курс математического анализа. Т.1 Дифференциальное и интегральное исчисление функции одной переменной. Ряды.: Учебник – 3-е изд., перераб. – М.: ФИЗМАТЛИТ, 2002. – 400 с.

6. Фихтенгольц Г.М. Курс дифференциального исчисления: в 3-х томах. Т. 1. / Г.М. Фихтенгольц; ред. А.А. Флоринского. – 8-е изд. М.: ФИЗМАТЛИТ: Лаборатория знаний, 2003 – 680 с. (Рекомендован Министерством образования Российской Федерации в качестве учебника для студентов физических и механико-математических специальностей высших учебных заведений).

7. Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов/ В.С. Шипачев. – 3-е изд., стер. – М.: Высшая школа, 2003. – 304 с.

Дата добавления: 2014-11-25