КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
СТАТИКА 1 страница
|
|
|
|
В задачах статики рассматривается равновесие тела под действием различных систем сил. Это позволяет привести общие для всех задач сведения справочного характера и сформулировать алгоритм методики подхода к задаче, пояснений в задаче и решения.
ВИДЫ СВЯЗЕЙ
Связь – тело, препятствующее перемещению данного объекта (тела, узла) в пространстве.
Реакция связи – сила, с которой связь действует на объект.
| Вид связи | Направление реакции связи | ||
Гладкая поверхность, на которую объект опирается в точке.

| Реакция гладкой поверхности направлена по нормали к поверхности опоры (если опора представляет собой острие, угол, линию, то реакция направлена по нормали к поверхности объекта) | ||
Острие, угол, линия (гладкие)

| Реакция направлена по нормали к поверхности объекта | ||
Гибкая связь (трос, цепь, нить).
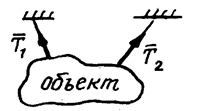
| Реакция гибкой связи направлена вдоль связи от объекта (нить растянута) | ||
Цилиндрический шарнир и подшипник
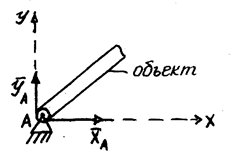
| Реакция цилиндрического шарнира расположена в плоскости, перпендикулярной оси шарнира, направление в плоскости не определено, указываем составляющие реакции. | ||
Катки (подвижный шарнир) без трения
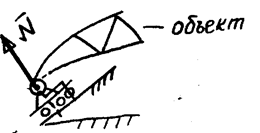
| Реакция связи направлена по нормали к поверхности опоры катков. | ||
Невесомый стержень, концы которого закреплены шарнирами.
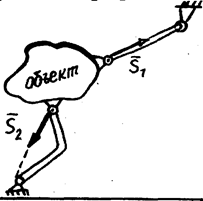
| Реакция связи направлена вдоль прямой, проходящей через концы стержня. Указываем от объекта, предполагая, что стержень растянут; минус в ответе означает, что стержень сжат. | ||
Подшипник и сферический шарнир

| Направление реакции не определено в пространстве, указываем три составляющие. | ||
| В случае плоской системы сил на объект действует сила, направление которой в плоскости действия сил не определено, и пара сил в этой плоскости. В случае пространственной системы сил на объект действует сила, направление которой в пространстве не, и пара сил, направление вектора момента которой в пространстве не определено. |
ОСНОВНЫЕ ПОНЯТИЯ
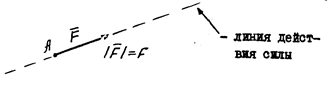
| Сила, действующая на твердое тело – скользящий вектор |

| Проекция силы на ось
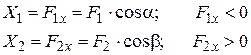
|
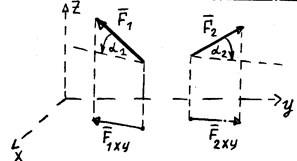
| Проекция силы на плоскость

|

| Момент силы относительно центра (точки)
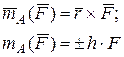 Знак
Знак 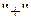 соответствует повороту тела вокруг центра А против хода часовой стрелки;
h – перпендикуляр, опущенный из центра А на линию действия силы (плечо силы) соответствует повороту тела вокруг центра А против хода часовой стрелки;
h – перпендикуляр, опущенный из центра А на линию действия силы (плечо силы)
|
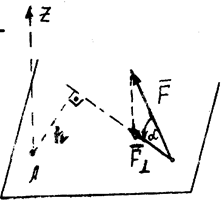
| Момент силы относительно оси
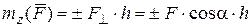 , ,
 – проекция силы на плоскость,
перпендикулярную оси;
А – точка пересечения оси с этой же плоскостью;
h – плечо силы – проекция силы на плоскость,
перпендикулярную оси;
А – точка пересечения оси с этой же плоскостью;
h – плечо силы 
|
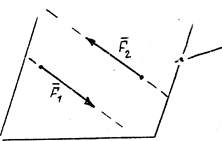
| Пара сил 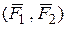 – две равные антипараллельные силы: – две равные антипараллельные силы:
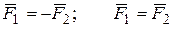
|
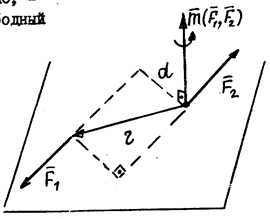
| Действие пары сил полностью характеризуется вектором-моментом пары.
Момент пары сил, действующей на твердое тело – свободный вектор.
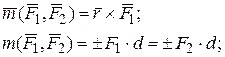
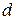 – плечо пары сил (перпендикуляр, опущенный из точки приложения силы на линию действия другой силы) – плечо пары сил (перпендикуляр, опущенный из точки приложения силы на линию действия другой силы)
|
ВИДЫ СИСТЕМ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО,
И УРАВНЕНИЯ РАВНОВЕСИЯ
| Произвольная пространственная система сил – линии действия сил расположены в пространстве | Векторная форма:
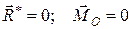 Координатная форма (аналитическая):
Координатная форма (аналитическая):
| ||||||||||||||||
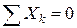
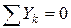
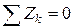
| 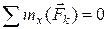
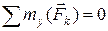
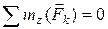
| ||||||||||||||||
| Система сходящихся сил – линии действия сил пересекаются в одной точке | Векторная форма:
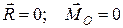 Координатная форма:
Координатная форма:
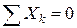 ; ;
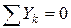 ; ;
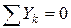
| ||||||||||||||||
| Пространственная система параллельных сил – линии действия сил в пространстве параллельны | Векторная форма:
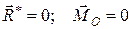 Координатная форма (ось
Координатная форма (ось  параллельна линиям действия сил): параллельна линиям действия сил):
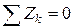 ; ;
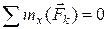 ; ;
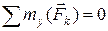
| ||||||||||||||||
| Произвольная плоская система сил – линии действия сил расположены в одной плоскости произвольно | Векторная форма:
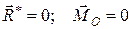 Координатная форма:
1-я форма (точка А – произвольная точка в плоскости):
Координатная форма:
1-я форма (точка А – произвольная точка в плоскости):
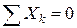 ; ; 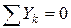 ; ; 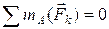 2-я форма (точки А, В, С не лежат на одной прямой):
2-я форма (точки А, В, С не лежат на одной прямой):
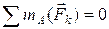 ; ; 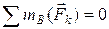 ; ; 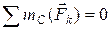 3-я форма (Ось ОХ не перпендикулярна прямой АВ):
3-я форма (Ось ОХ не перпендикулярна прямой АВ):
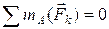 ; ; 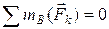 ; ; 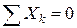
| ||||||||||||||||

   

   
  Плоская система параллельных сил – линии действия сил параллельны друг другу и расположены в одной плоскости Плоская система параллельных сил – линии действия сил параллельны друг другу и расположены в одной плоскости
| Векторная форма:
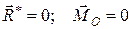 Координатная форма (ось Х параллельна линиям действия сил):
Координатная форма (ось Х параллельна линиям действия сил):
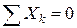 ; ;
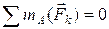
|
Все задачи статики (С1, С2, С3) относятся к теме о равновесии тела под действием различных систем сил. Это позволило сформулировать общий алгоритм методики подхода к задачам, пояснений к задачам и их решений.
Задача С1 потребует намного больше времени, так как последующие задачи включают весь материал этой задачи плюс новые теоретические сведения и их применение. Кроме того, с первой задачи приходится усваивать не только новый материал, но и терминологию данного предмета.
Примерный план (алгоритм) решения задач статики:
1. Назвать (выделить) объект: тело, узел, равновесие которого надо рассмотреть в данной задаче.
2. Указать на рисунке силы, действующие на этот объект:
а) активные силы;
б) назвать каждую связь и пояснить направление реакций связи или их составляющих (мысленно освобождая объект от связи на основании аксиомы освобождения от связей);
3. Назвать вид полученной системы сил, учитывая расположение линий действия сил.
4. Сформулировать условия равновесия полученной системы сил в алгебраической (координатной) форме.
5. Провести на рисунке координатные оси (если заранее не потребовалось это сделать).
6. Составить уравнения равновесия.
7. Решить систему уравнений с пояснением.
8. Сделать проверку.
9. Записать ответ.
При работе необходимо использовать учебник, данное пособие и справочник по математике.
Задача С1
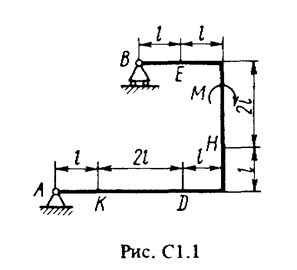
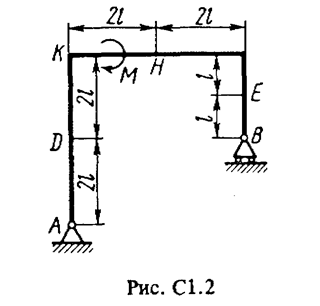
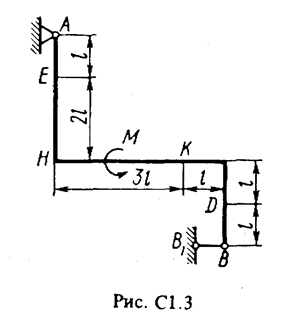
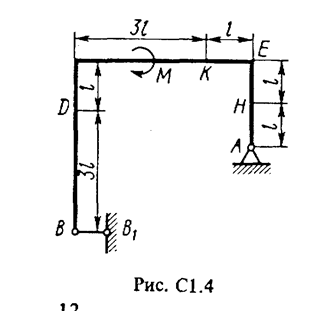
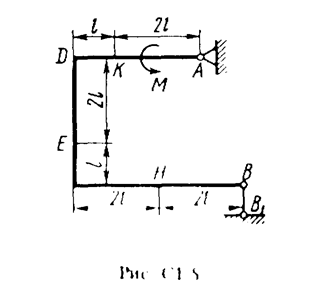
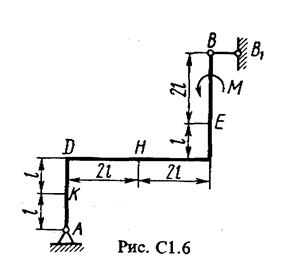
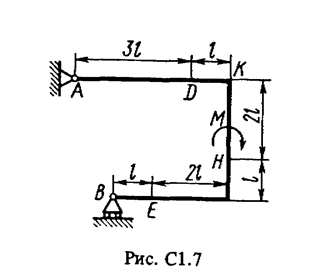
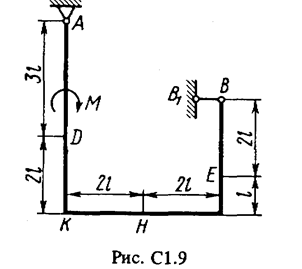
Жесткая рама (рис. С1.0-С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню ВВ1, или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.
На раму действуют пара сил с моментом М = 100 Н×м и две силы, значения которых, направления и точки приложения указаны в таблице (например, в условиях № 1 на раму действуют сила F1 = 10 Н под углом 30° к горизонтальной оси, приложенная в точке К, и сила F4 =40 Н под углом 60° к горизонтальной оси, приложенная в точке Н).
Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять l = 0,5 м.
Указания. Задача C1 - на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей (в данном случае относительно точки А). При вычислении момента какой-либо силы 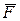 часто удобно разложить ее (согласно аксиоме параллелограмма сил) на составляющие
часто удобно разложить ее (согласно аксиоме параллелограмма сил) на составляющие  и
и 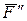 (не обязательно параллельно координатным осям), так, чтобы плечи этих составляющих определялись легче, чем плечо силы
(не обязательно параллельно координатным осям), так, чтобы плечи этих составляющих определялись легче, чем плечо силы 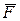 . После этого воспользоваться теоремой Вариньона в алгебраической форме:
. После этого воспользоваться теоремой Вариньона в алгебраической форме:
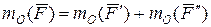 .
.

| 
|
| 
|
| 
|
| 
|

| 
|
Таблица С1
| Сила | 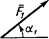
| 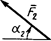
| 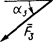
| 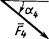
| ||||
| Номер условия | F1 = 10 H | F2 = 20 H | F3 = 30 H | F4 = 40 H | ||||
| Точка прилож. | 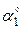
| Точка прилож. | 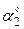
| Точка прилож. | 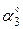
| Точка прилож. | 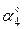
| |
| - | - | D | E | - | - | |||
| K | - | - | - | - | H | |||
| - | - | H | K | - | - | |||
| D | - | - | - | - | E | |||
| - | - | K | E | - | - | |||
| H | - | - | D | - | - | |||
| - | - | E | - | - | K | |||
| D | - | - | H | - | - | |||
| - | - | H | - | - | D | |||
| E | - | - | - | - | K |
Перед выполнением задания прочтите по учебнику темы: «Основные понятия и аксиомы статики», «Связи и реакции связей», «Плоская система сил», «Пара сил».
Вопросы, на которые следует обратить внимание и выучить:
1. Сила, линия действия силы.
2. Проекция силы на ось. В каком случае проекция силы на ось равна нулю?
3. Проекция силы на плоскость, в каком случае эта проекция равна нулю. Отличие проекции силы на плоскость от проекции силы на ось.
4. Алгебраической момент силы относительно центра (точки). В каком случае момент силы относительно центра равен нулю?
5. Что называется связями, перечислите виды связей.
6. Аксиома освобождения от связей.
7. Реакция связи, ее направление и точка приложения.
8. Какая система сил называется плоской (произвольной плоской)? Условия равновесия плоской системы сил в алгебраической (координатной) форме.
9. Теорема Вариньона в алгебраической форме.
Пример C1. Жесткая пластина ABCD (рис. C1) имеет в точке А неподвижную шарнирную опору, а в точке В - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

| Дано: F = 25 кН, a = 60°, Р = 18 кН, g = 75°, М = 50 кН × м, b =30°, l = 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками. |
Решение. 1. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы:
а) активные силы (нагрузки): силу 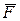 и пару сил с моментом М;
и пару сил с моментом М;
б) реакции связей:
в точке А связью является неподвижная шарнирная опора, ее реакцию изображаем двумя составляющими 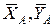 , параллельными координатным осям;
, параллельными координатным осям;
в точке В связью является подвижная шарнирная опора на катках, ее реакция направлена перпендикулярно плоскости опоры катков;
в точке D связью является трос, реакция троса 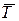 направлена вдоль троса от пластины (по модулю Т = Р).
направлена вдоль троса от пластины (по модулю Т = Р).
2. Для полученной плоской системы сил составим три уравнения равновесия. Первые два уравнения выражают равенство нулю алгебраических сумм проекций всех сил на оси координат х и у:
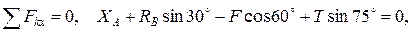 (1)
(1)

 (2)
(2)
Третье уравнение выражает равенство нулю алгебраической суммы моментов всех сил относительно произвольной точки тела. Для уменьшения числа неизвестных реакций связей в этом уравнении выбираем точку, через которую проходят линии действия двух неизвестных сил (точку А). При вычислении момента силы 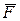 относительно точки А разложим силу
относительно точки А разложим силу 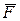 на составляющие
на составляющие 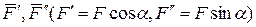 и воспользуемся теоремой Вариньона в алгебраической форме:
и воспользуемся теоремой Вариньона в алгебраической форме: 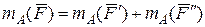 . Получим
. Получим
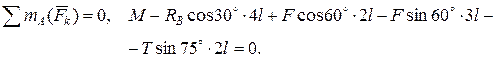 (3)
(3)
Решение системы уравнений начинаем с уравнения (3), так как оно содержит одну неизвестную 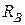 :
:

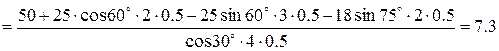 кН.
кН.
Подставляем 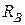 в уравнение (1):
в уравнение (1):
 .
.
Подставляем 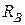 в уравнение (2):
в уравнение (2):
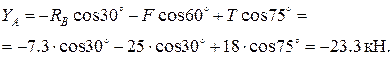
Проверка. Для проверки можно составить уравнение моментов относительно любой другой точки (кроме А). Желательно выбрать точку, относительно которой имеют моменты все три неизвестные силы (например, точку Е).
Составим уравнение 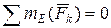 и подставим в него найденные реакции связей. Если задача решена верно, то сумма моментов всех сил должна быть близка к нулю (разница между суммой положительных чисел и модулем суммы отрицательных чисел не должна превышать 1% от этих величин).
и подставим в него найденные реакции связей. Если задача решена верно, то сумма моментов всех сил должна быть близка к нулю (разница между суммой положительных чисел и модулем суммы отрицательных чисел не должна превышать 1% от этих величин).
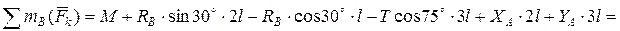
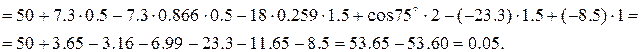
Погрешность расчета составляет 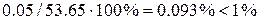 .
.
Ответ: ХА = -8,5 кН, YA = -23,3 кН, RB = 7,3 кН. Знаки указывают, что составляющие реакции шарнира 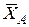 и
и 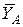 направлены противоположно показанным на рис. C1.
направлены противоположно показанным на рис. C1.
В примерах выполнения последующих задач решение уравнений и проверка не приводятся, но это необходимо делать при выполнении каждой задачи контрольной работы.
КИНЕМАТИКА
Задача К1
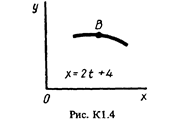
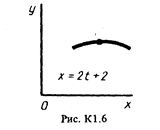
Точка В движется в плоскости ху (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1 (t), у = f2 (t), где х и у выражены в сантиметрах, t -в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1с определить координаты, скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Выполнить рисунок на странице в клетку или на вклеенном листке миллиметровой бумаги, на котором изобразить:
а) траекторию точки и ее координаты для заданного момента времени (в масштабе координат);
б) проекции скорости точки на оси координат и вектор скорости точки для заданного момента времени (в масштабе скоростей), причем полученный вектор скорости должен быть направлен по касательной к траектории;
в) проекции ускорения точки на оси координат и вектор ускорения точки для заданного момента времени (в масштабе ускорений), причем полученный вектор ускорения должен быть направлен в сторону вогнутости траектории (для прямолинейной траектории – вдоль этой прямой);
г) проекции вектора ускорения на касательную и нормаль (касательное и нормальное ускорения), определить их значения с помощью масштаба ускорений и сравнить со значениями, вычисленными по формулам.
д) отложить по нормали радиус кривизны в масштабе координат и показать центр кривизны траектории для данной точки (если позволяют размеры рисунка, в противном случае указать, что центр кривизны находится за пределами рисунка.
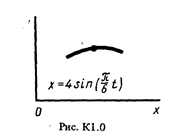
| 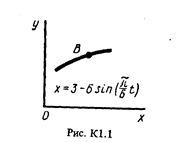
|

| 
|
| 
|
| 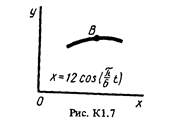
|
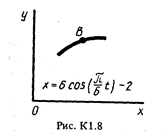
| 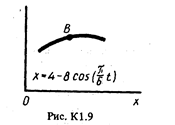
|
Таблица К1
| Условия | y = f2 (t) | ||
| Рис. 1-2 | Рис.3-6 | Рис.7-9 | |
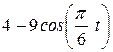
| 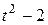
| 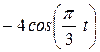
| |
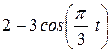
| 
| 
| |
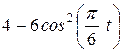
| 
| 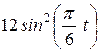
| |
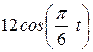
| 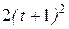
| 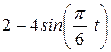
| |
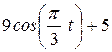
| 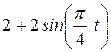
| 
| |
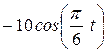
| 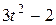
| 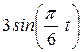
| |
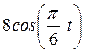
| 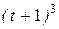
| 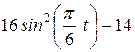
| |

| 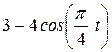
| 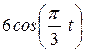
| |
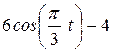
| 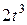
| 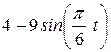
| |
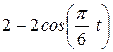
| 
| 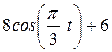
|
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1044; Нарушение авторских прав?; Мы поможем в написании вашей работы!