Статика и Кинематика

Решение. Для определения искомых реакций рассмотрим движение механической системы, состоящейиз вала АВ, стержня OD и груза, и применим принцип Даламбера. Проведем вращающиеся вместе с валомосиАху так, чтобы стержень лежал в плоскости ху, и изобразим действующие на систему внешние силы: силы тяжести, составляющие реакции подпятника и реакцию подшипника.

Согласно принципу Даламбера присоединим к этим силам силы инерции элементов стержня и груза, считая груз материальной точкой. Так как вал вращается равномерно (w = const), то элементы стержня имеют только нормальные ускорения 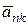направленные к оси вращения, а численно 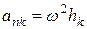, где h_k - расстояние элемента от оси. Тогда силы инерции 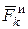будут направлены от оси вращении и численно , где D m - масса элемента. Поскольку все 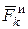пропорциональны h_k, то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей , линия действия которой проходит через центр, тяжести этого треугольника, т.е. на расстоянии H ₁ от вершины О, где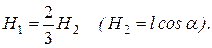

Но, как известно, равнодействующая любой системы сил равна ее главному вектору, а численно главный вектор сил инерции стержня 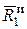= m ₁ a _C, где а _C ускорение центра масс стержня; при этом, как и для любого элемента стержня, а _C = а _Cn = w ² h _C = w ² OC sin a (OC= l/ 2). В результате получим

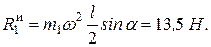
Аналогично для силы инерции 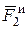груза найдем, что она тоже направлена от оси вращения, а численно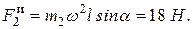

Так как все действующие силы и силы инерции лежат в плоскости ху, то и реакции подпятника А и подшипника В тоже лежат в этой плоскости, что было учтено приих изображении.

По принципу Даламбера, приложенные внешние силы и силы инерции образуют уравновешенную систему сил. Составляя для этой плоской системы сил три уравнения равновесия, получим:

(1)

(2)

(3)

Подставив сюда числовые значения всех заданных и вычисленных величин и решив эту систему уравнений, найдем искомые реакции.

Ответ: X_A =-11,8 Н, Y_A =49,1 Н, X_B =-19,7 Н.

Знаки указывают, что силы 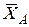и направлены противоположно показанным на рис. Д4.

6. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Теоретическая механика. Механическое движение. Разделы теоретической механики.

2. Предмет статики. Основные понятия статики (абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, внешние и внутренние силы). Аксиомы статики.

3. Несвободное твердое тело. Связи и реакции связей.

4. Проекция силы на ось и на плоскость. Алгебраический момент силы относительно точки. Момент силы относительно центра как вектор.

5. Выражение момента силы в виде векторного произведения. Аналитические формулы для вычисления моментов силы относительно координатных осей.

6. Момент силы относительно оси.

7. Связь момента силы относительно центра и оси, проходящей через этот центр.

8. Пара сил. Момент пары как вектор. Свойства пар.

9. Теорема о параллельном переносе силы.

10. Приведение произвольной системы сил к данному центру. Главный вектор и главный момент системы сил.

11. Условия равновесия систем сил.

12. Центр тяжести твердого тела и его координаты.

13. Центр тяжести объема, площади и линии.

14. Определение центра тяжести дуги окружности.

15. Определение центра тяжести треугольника и кругового сектора.

16. Теорема Вариньона.

17. Теорема о трех силах.

18. Предмет кинематики. Векторный способ задания движения точки. Траектория точки. Определение скорости и ускорения при векторном способе задания движения точки.

19. Координатный способ задания движения точки. Определение траектории, скорости и ускорения при этом задании.

20. Естественный способ задания движения точки. Естественный трехгранник. Определение скорости.

21. Определение нормального, касательного и полного ускорений при естественном способе задания движения точки.

22. Частные случаи движения точки по траектории. Равномерное и равнопеременное движение точки.

23. Поступательное движение твердого тела. Теорема о поступательном движении.

24. Вращательное движение тела вокруг неподвижной оси. Уравнение вращательного движения. Угловая скорость и угловое ускорение.

25. Равномерное и равнопеременное вращение твердого тела. Скорость и ускорение точек твердого тела при вращении.

26. Угловая скорость и угловое ускорение как векторы. Скорость точки вращающего тела в виде векторного произведения.

27. Выражения касательного и нормального ускорений точки вращающегося тела в виде векторного произведения.

28. Плоское движение твердого тела и движение плоской фигуры в ее плоскости. Уравнения движения плоской фигуры.

29. Разложение движения плоской фигуры. Теорема о независимость угловых характеристик движения от выбора полюса.

30. Определение скоростей точек плоской фигуры методом полюса.

31. Теорема о проекциях скоростей двух точек плоской фигуры.

32. Мгновенный центр скоростей. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Частные случаи определения мгновенного центра скоростей.

33. Сложное движение точки. Абсолютное, переносное и относительное движения точки. Теорема сложения скоростей.

34. Теорема сложения ускорений (теорема Кориолиса). Ускорение Кориолиса, его физический смысл. Примеры определения.

35. Теорема сложения ускорений при переносном поступательном движении.

ДИНАМИКА

1. Законы Ньютона. Первая и вторая задачи динамики точки.

2. Интегрирование дифференциального уравнения одномерного движения точки в частных случаях.

3. Уравнение движения точки в неинерциальной системе отсчета. Силы инерции.

4. Внешние и внутренние силы в механической системе. Равенство нулю главного вектора и главного момента внутренних сил.

5. Центр масс механической системы. Теорема о движении центра масс. Следствия.

6. Количество движения механической системы. Выражение количества движения через скорость центра масс. Теорема об изменении количества движения. Следствия.

7. Кинетический момент механической системы относительно центра и оси. Теорема об изменении кинетического момента. Следствия.

8. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси.

9. Момент инерции тела относительно оси. Моменты инерции простейших тел (диск, стержень). Радиус инерции.

10. Теорема о моментах инерции относительно параллельных осей (теорема Гюйгенса - Штейнера).

11. Центробежные моменты инерции механической системы и твердого тела. Главные оси инерции. Центральный момент инерции механической системы.

12. Дифференциальные уравнения движения твердого тела в случаях поступательного, вращательного и плоского движений.

13. Элементарная работа силы (различные формы записи). Мощность. Работа силы на конечном перемещении.

14. Работа силы тяжести.

15. Работа упругой силы пружины.

16. Работа и мощность силы, приложенной к вращающемуся твердому телу.

17. Кинетическая энергия материальной точки и механической системы. Теорема об изменении кинетической энергии материальной точки.

18. Теорема об изменении кинетической энергии механической системы в дифференциальной и интегральной формах.

19. Кинетическая энергия твердого тела при поступательном, вращательном и плоском движениях.

20. Принцип Даламбера.

21. Вычисление реакций подшипников при равномерном вращении твердого тела вокруг неподвижной оси.

22. Возможные перемещения. Идеальные связи (определение, примеры). Принцип возможных перемещений.

23. Потенциальная энергия механической системы во внешнем силовом поле. Работа и мощность потенциальной силы.

24 Потенциальная энергия в поле силы тяжести.

25. Потенциальная энергия в поле упругой силы пружины.

27. Потенциальная энергия взаимодействия точек механической системы.

28. Полная энергия механической системы. Закон сохранения полной энергии.

29. Обобщенные координаты механической системы (определение, примеры). Число степеней свободы.

30. Классификация связей. Примеры.

31. Обобщенные силы (определение, примеры).

32. Уравнения Лагранжа для механической системы.

СОДЕРЖАНИЕ

1. Введение 3

2. Программа 3

3. Методические указания изучения дисциплины 8

4. Методические указания по практическим занятиям 10

5. Контрольные работы 17

6. Вопросы для самопроверки 46

Дата добавления: 2014-11-25