При найденном значении C2 , уравнение (11) дает

(12)

Умножая здесь обе части на dt и снова интегрируя, найдем

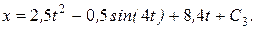(13)

Так как при t = 0 х = 0, то С ₃ = 0, и искомый закон движения груза будет

х = 2,5 t ² + 8,4 t - 0,5 sin (4 t), (14)

где х - в метрах, t - в секундах.

Задача Д3

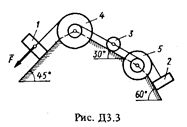
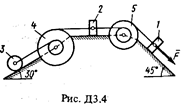
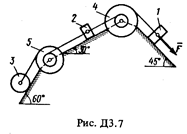
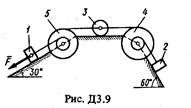
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R ₄ = 0,3 м, r ₄ = 0,1 м, R ₅ = 0,2 м, r ₅ = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0 – Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.

Под действием силы F = f (s), зависящей от перемещения точки при­ложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M ₄ и М ₅.

Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы равно s,. Искомая величина указана в столбце "Найти" таблицы, где обозначено: 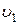- скорость груза 1, 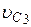- скорость центра масс катка 3, 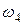- угловая скорость тела 4 и т.д.

Таблица Д3

Номер усло-вия	m 1, кг	m2, кг	m 3, кг	m 4, кг	m 5, кг	M 4, Н×м	M 5, Н×м	F = f(s)	s 1, м	Найти
							0,8	50(2+3 s)	1,0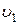
						0,6		20(5+2 s)	1,2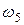
							0,4	80(3+4 s)	0,8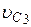
						0,3		40(4+5 s)	0,6
							0,6	30(3+2 s)	1,4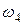
						0,9		40(3+5 s)	1,6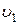
							0,8	60(2+5 s)	1,0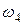
						0,6		30(8+3 s)	0,8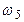
						0,3		40(2+5 s)	1,6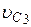
							0,4	50(3+2 s)	1,4

Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка, совершающего плоское движение, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s ₁, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Когда по данным таблицы m ₂ = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему.

Пример ДЗ. Механическая система (рис. ДЗ) состоит из сплошного цилиндрического катка l, ступенчатого шкива 2 с радиусами ступеней R ₂ и r ₂ (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.

Под действием силы F = f (s), зависящей от перемещения s точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент М 2 сил сопротивления. Дано: m 1 = 4 кг, m 2 = 10кг, m 3 = 8 кг, R 2 = 0,2 м, r 2 = 0,1м, f = 0,2. М 2 = 0,6 Н × м, F = 2(1+2 s) Н, s 1 = 2м. Определить: скорость центра масс катка, когда s = s 1.

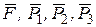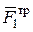Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из тел 1 2, 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные , момент сопротивления М ₂ реакции и силы трения и .

Для определения 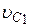воспользуемся теоремой об изменении кинетической энергии системы

(1)

2. Определяем Т ₀ и Т. Так как в начальный момент система находилась в покое, то Т ₀ = 0. Величина Т равна сумме энергий всех тел системы:

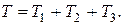(2)

Учитывая, что тело 1 совершает плоское движение, тело 3 движется поступательно, а тело 2 вращается вокруг неподвижной оси, получим

(3)

Все входящие сюда скорости следует выразить через искомую 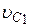. Приняв во внимание, что точка K ₁ - мгновенный центр скоростей катка 1, и обозначив радиус катка через r ₁, получим

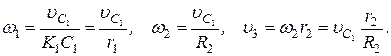(4)

Кроме того, входящие в (3) моменты инерции имеют значения

(5)

Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2) получим окончательно:

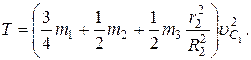(6)

3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С ₁ пройдет путь s ₁. Одновременно все перемещения следует выразить через заданную величину s ₁, для чего учтем, что здесь зависимость между перемещениями будет такой же, как и между соответствующими скоростями в равенствах (4), т.е. 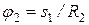. В результате получим:

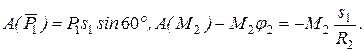
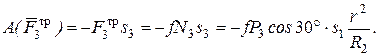
Работа остальных сил равна нулю, так как точка K ₁, где приложены силы и 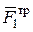, является мгновенным центром скоростей, точка O, где приложены 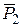, и , неподвижна, а реакция 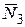перпендикулярна перемещению груза 3. Тогда окончательно

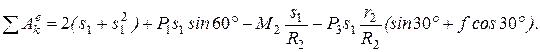(7)

4. Подставив выражения (6) и (7) в уравнение (1) и учитывая, что T ₀ = 0, получим

(8)

При числовых значениях заданных величин равенство (8) дает

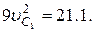
Отсюда находим искомую скорость.

Ответ: = 1.53м/с.

Задача Д4

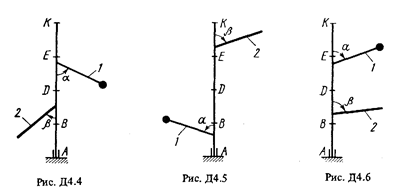
Вертикальный вал АК (рис. Д4.0-Д4.9, табл. Д4), вращающийся с постоянной угловой скоростью w = 10 с^-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д4 в столбце 2 (АВ = ВО = DE = EК = b). К валу жестко прикреплены невесомый стержень 1 длиной l ₁ = 0,4 м с точечной массой m ₁ = 6 кг на конце и однородный стержень 2 длиной l ₂ = 0,6 м, имеющий массу m ₂ = 4 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы a и b - в столбцах 5 и 6. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять b = 0,4 м.

Таблица Д4

Номер условия	Подшипник в точке	Крепление	a°	b°	Номер условия	Подшипник в точке	Крепление	a°	b°
стержня 1 в точке в точке	стержня 2 в точке в точке	стержня 1 в точке	стержня 2 в точке
	В	D	K				D	K	B
	D	D	E				E	B	K
	E	D	B				K	E	B
	K	D	E				D	E	K
	B	E	D				E	K	D

Указания. Задача Д4 - на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что когда силы инерции частиц тела (в данной задаче стержня 2) имеют равнодействующую , то численно = ma _C, где а _C - ускорение центра масс С стержня, но линия действия силы в общем случае не проходит через точку С (см. пример Д4).

Пример Д4. С невесомым валом АВ, вращающимся с постоянной угловой скоростью w, жестко скреплен стержень OD длиной l и массой m 1, имеющий на конце груз массой m 2 (рис.Д4). Дано: b 1 = 0,6 м, b 2 = 0,2 м, a = 30°, l = 0,5 м, m 1 = 3 кг, m 2 = 2 кг, w = 6 с^-1. Определить: реакции подпятника А и подшипника В.

Дата добавления: 2014-11-25