
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
СТАТИКА 2 страница
|
|
|
|
Зависимость х = f1, (t) указана непосредственно на рисунках, а зависимость у = f2 (t) дана в табл. К1 (для рис. О-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задачах C1, C2, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 - по последней.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки.
В данной задаче все искомые величины нужно определить только для момента времени t1 = 1 с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: cos 2a= 1 – 2sin2a = 2 cos2a- 1; sin 2a = 2sin a×cos a.
Пример К-1. Уравнения движения точки в плоскости заданы координатным способом и имеют вид:
 , (1)
, (1)
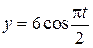 , (2)
, (2)
где время t задано в секундах, координаты x, y – в метрах.
Найти: уравнение траектории точки; положение точки на траектории при  (начальное положение) и при
(начальное положение) и при 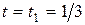 c; скорость
c; скорость 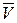 точки; ускорение
точки; ускорение  точки; касательное
точки; касательное  , нормальное
, нормальное  ускорения точки и радиус кривизны траектории
ускорения точки и радиус кривизны траектории 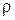 . В каждом пункте выполнить соответствующие построения на рисунке.
. В каждом пункте выполнить соответствующие построения на рисунке.
Решение. 1. Найдем уравнение траектории, исключив из (1) и (2) параметр t - время. Способ исключения t зависит от вида функций в правых частях (1), (2). В данном случае найдем из (1), (2) соответственно
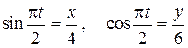 .
.
Возводя полученные соотношения в квадрат, после этого складывая их и учитывая, что  , найдем:
, найдем:
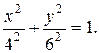
Из этого уравнения следует, что траекторией точки является эллипс, полуоси которого равны 4 м и 6 м, а центр имеет координаты (0, 0).
Выберем масштаб координат и выполним рисунок. Следует заметить, что приведенный рисунок (Рис. 1) имеет вид, соответствующий уже окончанию решения; свой рисунок рекомендуется делать по мере продвижения решения. Это позволяет контролировать получаемые результаты и делает их более наглядными.
2. Находим положение точки при 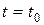 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):

3. Находим положение точки при 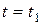 , подставляя это значение t в (1) и (2):
, подставляя это значение t в (1) и (2):

Указываем на рисунке точки 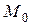 и
и 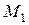 , учитывая масштаб координат.
, учитывая масштаб координат.
4. Найдем скорость точки. Из теории следует, что при координатном способе задания движения определяются сначала проекции скорости на оси координат. Используя (1) и (2) - уравнения движения точки - находим
 , (3)
, (3)
 . (4)
. (4)
Модуль скорости 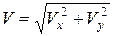 . Подставляя сюда (3), (4), получим
. Подставляя сюда (3), (4), получим
 . (5)
. (5)
При 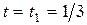 с:
с:  ,
,  ,
,
 . (6)
. (6)
 Рис. 1
Рис. 1
| Выберем масштаб для скоростей (рис.1), проведем в точке M 1 линии парал-лельные осям x и y, и на этих линиях в масштабе скоростей отложим отрезки: 5,44 по оси x и - 4,71 по оси y, что соответствует величи-нам и знакам найденных проекций скорости. На этих составляющих строим пара-ллелограмм (прямоуголь-ник), диагональ которого по величине и направлению соответствует вектору  .
Проверьте следующее: длина построенного вектора должна получиться равной найденному значению .
Проверьте следующее: длина построенного вектора должна получиться равной найденному значению 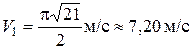
|
(с учетом масштаба скоростей). Вектор  направлен по касательной к траектории в точке
направлен по касательной к траектории в точке 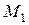 и показывает направление движения точки по траектории.
и показывает направление движения точки по траектории.
Удобно сейчас построить в точке 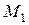 естественные оси: касательную
естественные оси: касательную  и главную нормаль
и главную нормаль 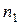 (они потребуются позже). Касательную
(они потребуются позже). Касательную  проводим вдоль
проводим вдоль  ; главную нормаль
; главную нормаль 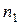 проводим перпендикулярно
проводим перпендикулярно  в плоскости рисунка и направляем к центру кривизны траектории в точке
в плоскости рисунка и направляем к центру кривизны траектории в точке 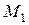 (в сторону вогнутости траектории).
(в сторону вогнутости траектории).
5. Находим ускорение точки, используя (3), (4):
 , (7)
, (7)
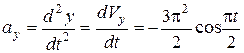 . (8)
. (8)
Модуль ускорения  . Из (7), (8) получим
. Из (7), (8) получим
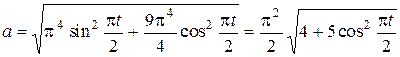 . (9)
. (9)
Подставляя в (7) - (9)  , найдем
, найдем
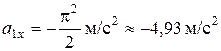 ,
, 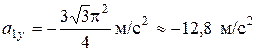 ,
,
 . (10)
. (10)
В точке 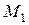 строим в масштабе проекции ускорений
строим в масштабе проекции ускорений 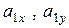 , учитывая их величины и знаки, а затем строим вектор ускорения
, учитывая их величины и знаки, а затем строим вектор ускорения 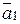 . Построив
. Построив 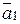 , следует проверить, получилось ли на рисунке
, следует проверить, получилось ли на рисунке  (c учетом масштаба ускорений), и направлен ли вектор
(c учетом масштаба ускорений), и направлен ли вектор 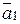 в сторону вогнутости траектории (вектор
в сторону вогнутости траектории (вектор 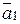 проходит через центр эллипса, но это есть особенность данной задачи, связанная с конкретным видом функций (1) и (2)).
проходит через центр эллипса, но это есть особенность данной задачи, связанная с конкретным видом функций (1) и (2)).
6. Находим касательное ускорение  , характеризующее изменение модуля
, характеризующее изменение модуля 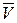 .
.
Учитывая (5), получим 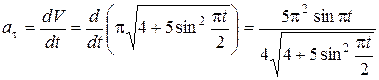 .
.
При 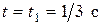
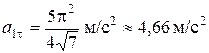 . (11)
. (11)
Касательное ускорение можно также найти, дифференцируя по времени равенство 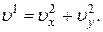 Получим
Получим
 , откуда следует
, откуда следует
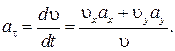
Нормальную составляющую 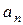 ускорения, характеризующую изменение направления
ускорения, характеризующую изменение направления 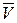 , можно найти по формуле
, можно найти по формуле
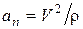 , (12)
, (12)
если 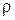 - радиус кривизны траектории заранее известен, или (учитывая, что,
- радиус кривизны траектории заранее известен, или (учитывая, что, 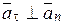 и, следовательно,
и, следовательно, 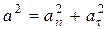 ) по формуле
) по формуле
 . (13)
. (13)
Так как в данной задаче радиус 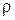 заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
заранее неизвестен, то используем (13). Подставляя (10), (11) в (13), получим
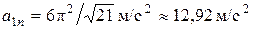 . (14)
. (14)
Вернемся к рис. 1. Ранее на этом рисунке вектор 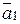 был построен по составляющим
был построен по составляющим 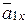 ,
,  . С другой стороны, этот вектор можно разложить на составляющие по естественным осям
. С другой стороны, этот вектор можно разложить на составляющие по естественным осям  и
и 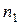 (пользуясь правилом параллелограмма). Выполним это разложение и построим на рисунке векторы
(пользуясь правилом параллелограмма). Выполним это разложение и построим на рисунке векторы  и
и 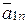 . Далее следует провести проверку: с учетом масштаба ускорений определить по рисунку величины
. Далее следует провести проверку: с учетом масштаба ускорений определить по рисунку величины 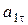 ,
,  и убедиться, что они совпадают с (11), (14).
и убедиться, что они совпадают с (11), (14).
Заметим, что движение точки ускоренное, т.к. направления векторов  и
и  совпадают (рис. 1).
совпадают (рис. 1).
Найдем радиус кривизны 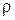 , используя (12), откуда следует, что
, используя (12), откуда следует, что 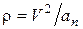 . Подставляя в последнее соотношение
. Подставляя в последнее соотношение  и
и  из (6) и (14), получим радиус кривизны траектории в точке
из (6) и (14), получим радиус кривизны траектории в точке 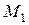 :
:  . Отложим на рисунке от точки
. Отложим на рисунке от точки 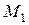 по оси
по оси 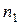 отрезок
отрезок 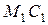 длины
длины  (в масштабе длин); полученная точка
(в масштабе длин); полученная точка 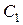 есть центр кривизны траектории в точке
есть центр кривизны траектории в точке 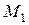 .
.
Объединяя полученные результаты, запишем ответ:
1. траектория точки - эллипс, имеющий уравнение  ;
;
2. 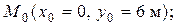 3.
3. 
4. 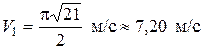 ;
;
5. 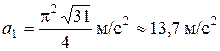 ;
;
6. 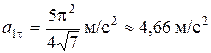 ;
; 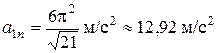 ;
;
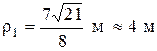 .
.
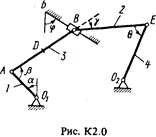
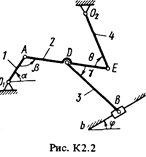
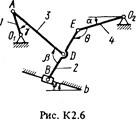
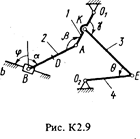
Задача К2
Плоский механизм состоит из стержней 1-4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О 2, шарнирами (рис. К2.0-К2.9). Длины стержней: l1 = 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,8 м. Положение механизма определяется углами a, b, g, j, q, которые вместе с другими величинами заданы в табл. К2. Точка D на всех риcyнках и точка K на рис. К2.7-К2.9 расположены в середине соответствующего стержня.
| 
|
| 
|

| 
|
| 
|

| 
|
Определить величины, указанные в таблице в столбце "Найти". Найти также ускорение аА точки А стержня 1, если стержень 1 имеет в данный момент времени угловое ускорение Î 1 = 10 с-2.
Таблица К2
условия | Углы | Дано | Найти | ||||||
| a° | b° | g° | j° | q° | w 1/с | w 1/с | u м/с | ||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 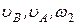
| |||||||
| - | - | 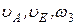
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
|
Дуговые стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т.е. по ходу или против хода часовой стрелки (например, угол g на рис. 1 следует отложить от стержня DE против хода часовой стрелки, а на рис. 2 - от стержня АЕ по ходу часовой стрелки).
Построение чертежа начинать со стержня, направление которого определяется углом a; ползун В и его направляющие для большей наглядности изобразить, как в примере К2 (см. рис. К2). Заданную угловую скорость считать направленной против хода часовой стрелки, а заданную скорость uВ- от точки В к b.
Указания. Задача К2 - на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
ПримерК2. Механизм (рис. К2, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами.

Дано: a = 120°, b = 60°, g = 90°, j = 0°, q = 30°. AD = DE, l 1 = 0,6 м, l 3 = 1,2 м, w 1 = 5 с-1, Î 1 =8 с-2.
Определить:  и аA.
и аA.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К2, б).
2. Определяем uE. Точка Е принадлежит стержню AЕ. Чтобы найти uE, надо знать скорость какой-нибудь другой точки этого стержня и направление uE. По данным задачи можем определить
 (1)
(1)
Направление  найдем, учтя, что точка Е принадлежит одновременно стержню 0 2 Е, вращающемуся вокруг О 2; следовательно,
найдем, учтя, что точка Е принадлежит одновременно стержню 0 2 Е, вращающемуся вокруг О 2; следовательно,  ^ 0 2 Е. Теперь, зная
^ 0 2 Е. Теперь, зная 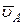 и направление
и направление  , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АЕ) на прямую, соединяющую эти точки (прямая АЕ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АЕ) на прямую, соединяющую эти точки (прямая АЕ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор  (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
 (2)
(2)
3. Определяем uВ. Точка В принадлежит стержню BD. Следовательно, по аналогии с предыдущим, чтобы определить uВ, надо сначала найти скорость точки D, принадлежащей одновременно стержню АЕ. Для этого, зная 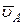 и
и  , построим мгновенный центр скоростей (МЦС) стержня АЕ; это точка С 2, лежащая на пересечении перпендикуляров к
, построим мгновенный центр скоростей (МЦС) стержня АЕ; это точка С 2, лежащая на пересечении перпендикуляров к 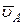 и
и  , восставленных из точек А и Е (к
, восставленных из точек А и Е (к 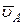 и
и  перпендикулярны стержни 1 и 4).По направлению вектора
перпендикулярны стержни 1 и 4).По направлению вектора 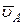 определяем направление поворота стержня АЕ вокруг МЦС С 2. Вектор
определяем направление поворота стержня АЕ вокруг МЦС С 2. Вектор 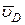 будет перпендикулярен отрезку С 2 D, соединяющему точки D и С 2, и направлен в сторону поворота. Величину
будет перпендикулярен отрезку С 2 D, соединяющему точки D и С 2, и направлен в сторону поворота. Величину  найдем из пропорции
найдем из пропорции
 (3)
(3)
Чтобы вычислить С 2 D и С 2 А, заметим, что D AС 2 E - прямоугольный, так как острые углы в нем равны 30 и 60°, и что С 2 А = AE sin 30° = 0,5 АЕ = AD. Тогда D AС 2 D является равносторонними С 2 А = С 2 D. В результате равенство (3) дает
 (4)
(4)
Так как точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно, то направление  известно. Тогда, восставляяиз точек В и D перпендикуляры к скоростям
известно. Тогда, восставляяиз точек В и D перпендикуляры к скоростям  и
и 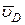 , построим МЦС С 3 стержня BD. По направлению вектора
, построим МЦС С 3 стержня BD. По направлению вектора 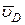 определяем направление поворота стержня BD вокруг центра С 3. Вектор
определяем направление поворота стержня BD вокруг центра С 3. Вектор  будет направлен в сторону поворота стержня BD. Из рис. К2, б видно, что Ð С 3 DB = 30°, a Ð D С 3 B = 90°, откуда С 3 B = l 3 sin 30°, С 3 D = l 3 cos 30°. Составив теперь пропорцию, найдем, что
будет направлен в сторону поворота стержня BD. Из рис. К2, б видно, что Ð С 3 DB = 30°, a Ð D С 3 B = 90°, откуда С 3 B = l 3 sin 30°, С 3 D = l 3 cos 30°. Составив теперь пропорцию, найдем, что

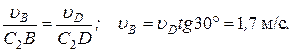 (5)
(5)
4. Определяем w3. Так как МЦС стержня 3 известен (точка С3), то

5. Определяем аA. Так как Î 1, известно, то аAt=l 1 Î 1. Далее  , или
, или 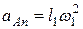 . Тогда
. Тогда 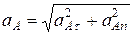 . Произведя вычисления, получим аА = 15,8 м/с2.
. Произведя вычисления, получим аА = 15,8 м/с2.
Ответ: uЕ = 5,2 м/с, uВ = 1,7 м/с, w3 = 2,9 с-1, аА = 15,8 /с2.
ДИНАМИКА
Задача Д1
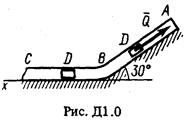
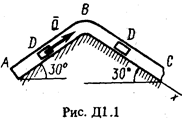
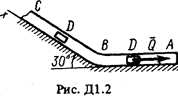
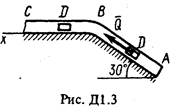
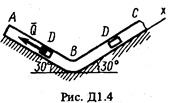
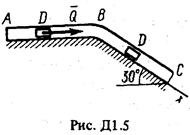
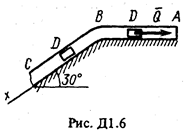
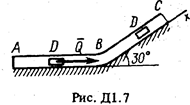
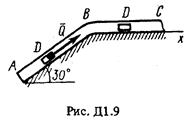
Груз D массой т, получив в точке А начальную скорость u 0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные,или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила  (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости
(ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости  груза (направлена против движения).
груза (направлена против движения).
| 
|
| 
|
| 
|
| 
|
| 
|
Таблица Д1
| Номер условия | m, кг | u0, м/с | Q, H | R, H | l, м | t 1, с | Fx,H |
| 2,4 | 0,8 u 2 | 1,5 | - | 4sin(4 t) | |||
| 0,4 u | - | 2,5 | -5 cos(4 t) | ||||
| 0,5 u 2 | - | 6t2 | |||||
| 1,8 | 0,3 u | - | -2 cos(2 t) | ||||
| 0,6 u 2 | - | -5sin(2 t) | |||||
| 4,5 | 0,5 u | - | 3 t | ||||
| 0,8 u 2 | 2,5 | - | 6 cos(4 t) | ||||
| 1,6 | 0,4 u | - | -3sin(4 t) | ||||
| 4,8 | 0,2 u 2 | - | 4 cos(2 t) | ||||
| 0,5 u | - | 4sin(2 t) |
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!