Электронная библиотека научной литературы по гуманитарным

Общая схема исследования ф-ции необходима для построения графика.

Экстремумы ф-ции нескольких переменных. Необходимые и достаточные признаки экстремума ф-ции 2х переменных.

Z=f(x,y), M₀(x₀,y₀), M(x,y)

Max ф-ции Z называется такое ее значение f(x₀,y₀), которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки M₀

Min ф-ции Z называется такое ее значение f(x₀,y₀), которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки M₀

Экстремум сущ. в тех точках, в которых частная производная ф-ции Z=0 или не существует:

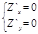
Если Z=f(x₁,x₂,...x_n), то ¶Z/¶x_i=0, i=1,2,...n - необходимое условие.

Достаточный признак:

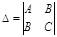
где A= Z``<sub>XX</sub>(x<sub>0</sub>,y<sub>0</sub>), C= Z``_yy(x₀,y₀), B= Z``_yx (x₀,y₀),

1) если D>0, то М₀ - точка экстремума;

если А<0 или С<0, то М₀ - точка max;

если А>0 или С>0, то М₀ - точка min.

2) если D<0, то экстремума нет

3) если D=0, то вопрос о существовании экстремума остается открытым.

Найти:
-обл. определения ф-ции

-точки разрыва и интервалы, где ф-ция явл-ся непрерывной

-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты

-т. пересечения графика с осями координат

-симметрия графика (чет./нечет):

f(-x)=x симметрична относительно осей

f(-x)=-x симметрична относительно О(0,0)

-периодичность

-интервалы монотонности

-точки экстремума

-наибольшее и наименьшее значение

-выпуклость, вогнутость

-точки перегиба

-поведение ф-ции в безконечности, наклонная и горизонтальные асимптоты

-нанесение на график.

дисциплинам www.vusnet.ru\biblio

Мы приглашаем Вас активно пользоваться Эл. библиотекой РГИУ. В Вашем распоряжении более 4000 полновесных текстов книг и статей, более 70 словарей. Любую книгу библиотеки вы можете свободно скачать и сохранить у себя на ПК.

Об учебном портале РГИУ. www.vusnet.ru

Если вы хотите получить первое или второе высшее образование, мы рекомендуем поступить учиться в РГИУ. Вы получите хорошее образование, гос.диплом аккредитованного Московский вуза, сэкономите временя и деньги.

Обучение проходит в Интернете, где Вам доступны учебники, специально подготовленные для чтения на ПК и тесты. К каждому учебнику прилагаются: хрестоматия, библиография, Интернет-ресурсы, специальные статьи, словари. Инвалидам скидка - 20%.

В учебном Портале РГИУ имеется 100 общеобразовательных и профессиональных курсов. Они в вашем распоряжении. www.vusnet.ru

Если у Вас возникли вопросы, постараемся на них ответить. Если есть пожелания – непременно сообщите.

Пожалуйста, пишите на: [e-mail], [e-mail] Или звоните: (905) 7211213 (Елена).

РОССИЙСКАЯ АКАДЕМИЯ ОБРАЗОВАНИЯ СЕВЕРО-ЗАПАДНОЕ ОТЕДЕЛЕНИЕ

СЕРИЯ

Дата добавления: 2014-11-25