Изучение степени тесноты связи между качественными признаками

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации ( ) и контингенции ( ).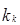

Для их вычисления строится таблица, показывающая связь между двумя явлениями, каждое из которых должно быть альтернативным:

а	b
с	d

Коэффициенты вычисляются по формулам

ассоциации: =

контингенции: =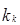

Связь между двумя качественными признаками считается подтвержденной, если > 0,5 или 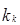> 0,3.

. Пример 3. Определить степень тесноты связи между успеваемостью студентов по математике и посещением занятий по этой же дисциплине.

Группы студентов	Численность студентов –всего, чел.	Из них
Успешно сдали экзамен	Не сдали экзамен
Посещающие занятия
Не посещающие занятия

Решение. Рассчитаем коэффициенты ассоциации и контин-генции

= = = = 0,86;

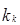= = = = 0,53.

Значения полученных коэффициентов ассоциации и контингенции свидетельствуют о тесной связи между успешной сдачей экзамена по математике студентом и его посещением занятий по этой же дисциплине. Для изучения тесноты связи между двумя качественными признаками, каждый из которых состоит из трех и более групп, вычисляют коэффициенты взаимной сопряженности Пирсона ( ) и Чупрова.

Для их вычисления строится вспомогательная таблица.

х у				Итого
II   III
Итого

Для вычисления этих коэффициентов определяют показатель взаимной сопряженности ( 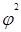) по формулам

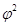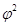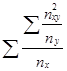= – 1 или = – 1.

Коэффициент Пирсона рассчитывается по формуле

= ;

Коэффициент Чупрова вычисляют по формуле

= ,

где – число групп первого признака;

– число групп второго признака.

Чем ближе величина коэффициентов Пирсона и Чупрова к 1, тем сильнее связь между признаками.

Пример 4. Оцените связь между уровнем жизни населения и уровнем экономического развития региона с помощью показателей Пирсона и Чупрова.

Группы регионов по уровню экономического развития	Группы регионов по уровню жизни населения	Итого
высокий	средний	низкий
Высокий
Средний
Низкий
Итого

Решение. Рассчитаем нужные показатели

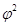= – 1 = (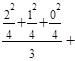 + 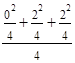) – 1 = = 1,367 – 1 = 0,367.

= = = 0,518.

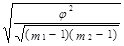= = = 0,428.

Значит, связь между уровнем экономического развития регионов и уровнем жизни населения в них средняя.

Задания для самостоятельного решения

1.По приведенным данным за 2002 г. оцените степень тесноты связи между численностью лиц, занятых в экономике, и объемом произведенного ВВП с помощью линейного коэффициента корреляции и ранговых коэффициентов связи.

Страна	Численность занятых в экономике, млн. чел.	Валовой внутренний продукт, млрд. долл. США (по ППС)
Великобритания	28,4	1572,0
Германия	36,5	2096,0
Италия	21,9	1468,0
Канада	15,4	911,0
Россия	65,8	1067,0
США	136,5	10020,0
Япония	63,3	3380,0

2.По приведенным данным с помощью эмпирического корреляционного отношения и линейного коэффициента корреляции определите, существует ли зависимость урожайности сельско-хозяйственных культур от количества внесенных минеральных удобрений в целом по РФ в 2006 г.

Культура	Внесено минеральных удобрений, кг/га	Урожайность, ц/га
Сахарная свекла		325,0
Зерновые		18,9
Картофель		130,0
Овощи и бахчевые		179,0
Лен-долгунец		6,1
Подсолнечник		11,4

3.По исходным данным задания 2:

а) постройте поле корреляции;

б) составьте уравнение линейной функции, выражающей связь между урожайностью сельскохозяйственных культур и количеством внесенных минеральных удобрений в целом по РФ в 2006 г., и изобразите ее графически.

4.По исходным данным задания 2 определите степень тесноты связи между этими показателями с помощью ранговых коэффициентов связи Спирмена и Кендалла.

5.Оцените степень тесноты связи между онкологической заболеваемостью и работой со свинцом работников одного из предприятий по приведенным данным (цифры условные).

Группы сотрудников	Обследовано сотрудников – всего, чел.	В том числе
больны онкологическими болезнями	здоровы
Работали со свинцом
Не работали со свинцом

6.Определите, на сколько процентов увеличится средний прогнозируемый уровень балансовой прибыли при увеличении стоимости реализации продукции на 1%, если уравнение регрессии уровня балансовой прибыли от уровня стоимости реализации 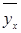= 20,0 + 1,5 . Известно, что средние значения факторного и результативного признака, соответственно, равны 6,2 млн. руб. и 460 млн. руб.

7.Имеются данные о среднегодовой численности работников и сальдированном финансовом результате деятельности предприятий (прибыль минус убытки) отдельных видов деятельности в 2006 г.

Вид деятельности	Среднегодовая численность работников, тыс. чел.	Сальдированный финансовый результат, млрд. руб.
Добыча полезных ископаемых		712,9
Производство кокса и нефтепродуктов		509,7
Химическое производство		84,8
Металлургическое производство	1 142	517,6
Производство и распределение электроэнергии, газа и воды	1 861	90,5

1. Составьте уравнение линейной функции, выражающей зависимость сальдированного финансового результата (прибыль минус убытки) от среднегодовой численности лиц, занятых в отраслях промышленности.

2. Определите степень тесноты связи между этими показателями с помощью эмпирического корреляционного отношения, линейного коэффициента корреляции и ранговых коэффициентов связи.

8.С помощью ранговых коэффициентов связи определите по следующим данным, существует ли связь между полом зрителей и выбором популярных передач (% к числу опрошенных):

Типы передач	Оценка популярности
мужчины	женщины
Кино- и телефильмы
Музыкальные программы
Информационные программы
Спортивные передачи
Юмористические программы
Викторины
Телеспектакли

9. Имеется уравнение регрессии уровня производительности труда от уровня фондоотдачи: = 232,0 + 15,2 .

Определите средний прогнозируемый уровень производи-тельности труда при уровне фондоотдачи, равном 4,5 руб.

10.По приведенным ниже данным оцените зависимость между уровнем образования работников фирмы и уровнем оплаты их труда (цифры условные).

Группы сотрудников фирмы по уровню образования	Численность сотрудников – всего, чел.	Из них
не довольны уровнем оплаты труда	довольны уровнем оплаты труда
Не имеют высшего образования
Имеют высшее образование

11. В результате наблюдения 6 000 чел. был установлен цвет волос и цвет глаз каждого человека. Необходимо выявить, существует ли связь между цветом волос и цветом глаз. Результаты наблюдения следующие:

Цвет глаз	Цвет волос
светлый	темный
Светлый	1 600	3 100
Темный		1 150

12. С помощью ранговых коэффициентов связи Спирмена и Кендалла определите, существует ли связь между числом организаций, выпускающих инновационную продукцию, и объемом инновационной продукции по отдельным видам экономической деятельности за 2005 г. в целом по РФ:

Вид экономической деятельности	Число организаций, выпускающих инновационную продукцию	Объем инновационной продукции, млрд. руб.
Добыча полезных ископаемых		67,3
Производство машин и оборудования		14,1
Производство транспортных средств		63,8
Производство электрооборудования		21,4
Производство кокса и нефтепродуктов		3,3

13. По исходным данным задания 12 с помощью линейного коэффициента корреляции определите степень тесноты связи между числом организаций, выпускающих инновационную продукцию, и объемом инновационной продукции по отдельным видам экономической деятельности за 2004 г. в целом по РФ.

14. По материалам выборочного обследования домашних хозяйств с помощью линейного коэффициента корреляции и ранговых коэффициентов Спирмена и Кендалла определите, существует ли связь между величиной среднедушевого денежного дохода и расходами домашних хозяйств на продукты питания (руб. в месяц):

Среднедушевой денежный доход, руб.	3 280	4 060	5 950	6 175	8 300
Расходы на продукты питания, руб.	1 470	1 960	2 202	2 840	3 655

15. По исходным данным задания 14 составьте уравнение линейной функции, выражающей зависимость объема расходов домашних хозяйств на продукты питания от величины среднедушевого денежного дохода (руб./ мес.)

16. По кредитным организациям в федеральных округах РФ приводятся следующие данные на начало 2006 г. (млрд. руб.):

Федеральный округ	Объем вкладов юридических и физических лиц	Средства юридических и физических лиц в рублях, привлеченные путем выпуска векселей	Активы
Центральный	1827,2	414,8	8358,9
Северо-Западный	364,6	23,3	451,1
Южный	204,4	1,8	89,2
Приволжский	446,3	31,8	357,9
Уральский	266,8	17,1	313,6
Сибирский	236,4	4,5	115,5
Дальневосточный	118,6	1,0	64,2

С помощью линейного коэффициента корреляции и ранговых коэффициентов связи определите, существует ли зависимость общей величины активов кредитных организаций от:

а) объема вкладов юридических и физических лиц;

б) средств юридических и физических лиц в рублях, привлеченных путем выпуска векселей.

17. Имеются следующие данные по группе работников предприятия (цифры условные):

Стаж работы, лет	5,0	6,0	7,0	8,5	10,0
Выработка продукции в расчете на 1 работника, шт.

Найдите уравнение корреляционной связи между стажем работы и выработкой продукции (связь в виде параболы второго порядка). Изобразите полученную связь графически.

18. По исходным данным задания 17 определите степень зависимости общей величины активов кредитных организаций от объема вкладов юридических и физических лиц и средств юридических и физических лиц в рублях, привлеченных путем выпуска векселей:

а) с помощью множественного коэффициента корреляции;

б)с помощью коэффициента конкордации.

19. Приводится распределение работников одного из промышленных предприятий по уровню образования и категории работников.

Уровень образования	Категории работников
руководители	специалисты	служащие	рабочие
Высшее
Незаконченное высшее
Среднее специальное
Среднее общее
Неполное среднее	–

Рассчитайте коэффициенты Пирсона и Чупрова.

20. Приводятся следующие данные о семейном положении и поле лиц, занятых в экономике региона (тыс. чел.) в 2005 г. (цифры условные):

Пол	Семейное положение
состоят в браке	холосты, не замужем	вдовцы, вдовы	разведены
Мужчины Женщины	72,4 63,8	19,7 14,0	1,2 6,6	6,7 15,8

Определить степень тесноты связи между полом работника и состоянием его в браке.

21.По следующим данным постройте уравнение линейной функции и рассчитайте линейный коэффициент корреляции

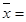59,4125; 28,7; 1889,575;

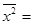3971,16125; 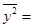903,9425; = 3,925.

22. Приводятся следующие данные об объеме отгруженной продукции, продукции сельского хозяйства, обороте розничной торговли и сальдированном финансовом результате (прибыль минус убытки) по отдельным регионам РФ в 2005 г. (млрд. руб.):

Регион	Объем отгруженной продукции	Продукция сельского хозяйства	Оборот розничной торговли	Сальдированный финансовый результат
Краснодарский край
Республика Башкортостан
Нижегородская область
Самарская область
Тюменская область	1 837
Свердловская область
Пермский край

С помощью эмпирического корреляционного отношения, линейного коэффициента корреляции и ранговых коэффициентов связи определите степень тесноты связи:

а) между объемом промышленной продукции и сальдированным финансовым результатом;

б) между объемом продукции сельского хозяйства и сальдированным финансовым результатом.

23. По исходным данным задания 22 с помощью известных методов определите степень зависимости сальдированного финансового результата одновременно от трех факторов: объема промышленной продукции, объема продукции сельского хозяйства и оборота розничной торговли.

24.Приводятся следующие данные по кредитным организациям отдельных регионов РФ на начало октября 2006 г.:

Регион	Активы, млрд. руб.	Объем вкладов юридических и физических лиц, млрд. руб.	Прибыль, млрд. руб.
Центральный	10697,0	2256,9	236,6
Северо-Западный	513,2	445,0	14,4

О к о н ч а н и е

Южный	112,0	252,2	2,6
Приволжский	460,1	543,1	8,5
Уральский	387,8	308,2	6,3
Сибирский	154,7	277,6	3,4
Дальневосточный	82,7	141,7	1,8

С помощью эмпирического корреляционного отношения, линейного коэффициента корреляции и ранговых коэффициентов связи определите степень тесноты связи между:

а) активами кредитных организаций и величиной полученной прибыли;

б) объемом вкладов юридических и физических лиц и величиной полученной прибыли;

в) объемом вкладов юридических и физических лиц и активами кредитных организаций.

25. По исходным данным задания 24 с помощью известных методов определите степень зависимости величины полученной прибыли одновременно за счет двух факторов: активов кредитных организаций и объема вкладов юридических и физических лиц.

Контрольные вопросы

1. В чем заключается корреляционно-регрессионный анализ?

2. Как классифицируют связь между признаками?

3. Как графически можно определить степень тесноты связи между двумя количественными признаками?

4. Что характеризуют эмпирическое корреляционное отношение и линейный коэффициент корреляции?

5. По каким формулам рассчитывают линейный коэффициент корреляции?

6. Какие вы знаете ранговые коэффициенты связи? В каких случаях они применяются? Как они вычисляются и что характеризуют?

7. Какие показатели применяются для определения степени тесноты связи между двумя качественными признаками?

СПИСОК ЛИТЕРАТУРЫ

Дата добавления: 2014-11-25