Блуждания молекул и… людей

Опыты с йодом позволяют проникнуть в то, как движутся молекулы в результате диффузии в воздухе и в «свободном полете» в вакууме. Если на дно пробирки поместить кристаллический йод и начать нагревать его, то снизу будут подниматься тяжелые фиолетовые пары, которые медленно заполнят пробирку, частично оседая на более холодных стенках в виде мелких кристалликов. Если же поместить кристаллы йода на дно стеклянной ампулы, выкачать из нее с помощью хорошего насоса воздух до очень малого остаточного давления, а потом герметично запаять, то при нагревании донышка ампулы никаких паров в ней не замечается, но на холодных стенках немедленно начинают оседать мельчайшие серые кристаллики йода. Если в ампуле находится не мелкий порошок йода, а один крупный кристалл (такой кристалл вырастет сам по себе, если вакуумированную ампулу оставить в покое на несколько месяцев), то при нагревании донышка ампулы небольшим пламенем кристалл начинает смешно дрожать и подпрыгивать. А так как йод очень тяжелый (плотность 4,94 г/см3, почти вдвое больше, чем у гранита), в тишине отчетливо слышен стук. Как объяснить все эти явления?

При нагревании кристалла молекулы йода начинают намного быстрее отрываться от его поверхности. Если в ампуле воздух, то из‑за столкновений с молекулами О2 и N2 молекулы I2 могут снова вернуться и прилипнуть к поверхности. Если же в сосуде вакуум, такого шанса у молекул йода нет, и они будут лететь прямолинейно и равномерно, пока не столкнутся со стенкой, к которой и прилипнут (стенка холодная).

Быстро ли летят молекулы? Эта задача была решена еще в XIX в., когда трудами Джеймса Максвелла, Людвига Больцмана, других ученых была создана молекулярно‑кинетическая теория газов. В соответствии с этой теорией средняя скорость молекул

, где М – молекулярная масса газа (кг/моль), R – газовая постоянная (8,31 Дж/(моль К)), T – абсолютная температура. Как известно, кинетическая энергия тела, в том числе и молекулы, определяется формулой Е = Mu 2/2. Подставляя в эту формулу выражение для u, получаем: Е = 3 RТ /2, т. е. энергия молекул не зависит от их массы, а только от температуры. По этому поводу Максвелл в своем докладе «Пояснения к динамической теории газов», сделанном в 1859 г., сказал: «Динамическая теория говорит нам также и о том, что происходит, когда молекулы различных масс сталкиваются друг с другом. Бо́льшие массы будут двигаться медленнее меньших, так что в среднем каждая молекула, большая или малая, будет иметь ту же энергию движения».

Если в формулу для средней скорости молекул подставить приведенное значение R, а молекулярную массу выражать в более привычных для химиков единицах (г/моль), то получим формулу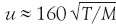

. По этой формуле нетрудно рассчитать, с какой скоростью движутся в газе разные молекулы. Сразу видно, что чем выше температура и чем легче молекулы, тем быстрее они движутся. Но эта зависимость не очень сильная, так как величины М и Т находятся под знаком корня.

Рассчитаем, например, с какой скоростью движутся при комнатной температуре (Т = 293 К) молекулы самого легкого газа, водорода, – М = 2 г/моль. Из формулы получаем удивительный результат: u = 1,94 км/с – намного быстрее пули! Самые тяжелые молекулы UF6 с М = 352 (это вещество в виде газа используют для разделения изотопов урана) движутся при комнатной температуре, со средней скоростью около 145 м/с. Небольшое повышение температуры, как следует из формулы, увеличивает скорость молекул не очень сильно. Так, при 55 °С (328 К) давление паров над UF6 достигает 1 атм, и при этой температуре молекулы вещества в газе движутся со средней скоростью около 155 м/с, т. е. лишь немного быстрее.

Молекулы йода – одни из самых тяжелых (М = 254), и их средняя скорость равна примерно 170 м/с при 20 °С. Теперь понятно, почему мы не видим паров йода при его возгонке в вакууме: даже тяжелые молекулы движутся слишком быстро, достигают стенки за время меньше одной тысячной секунды, и их невозможно увидеть – как не видно летящие пули. Расчет показывает, что пары при возгонке йода в вакууме станут видны, если каждую секунду с поверхности будет испаряться 1 г вещества! Такой скорости в ампуле достичь невозможно, так как при нагревании донышка ампулы теплота передается только нижней поверхности кристалла, который тут же и испаряется, отбирая при этом тепловую энергию.

Испарение в вакууме именно нижней части большого кристалла при сильном нагревании донышка ампулы объясняет и подпрыгивание этого кристалла. Вылетающие вниз с большой скоростью молекулы I2 создают реактивную тягу, приподнимающую кристалл. Но как только кристалл отрывается от горячей поверхности, он немного остывает, скорость испарения снижается, и кристалл падает на дно. После этого процесс повторяется.

Посмотрим теперь, что происходит при нагревании кристаллического йода в ампуле с воздухом. Молекулы I2, оторвавшись от поверхности и летя с огромной скоростью, тем не менее не могут улететь далеко, так как тут же сталкиваются с молекулами воздуха, которых огромное количество: примерно 2,5 · 1019 в 1 см3 при комнатной температуре и давлении 1 атм. После каждого столкновения молекула случайным образом изменяет направление своего движения, пролетая в среднем от одного столкновения до другого небольшое расстояние λ. Оказывается, путем простых экспериментов можно определить это расстояние (оно называется свободным пробегом), а также рассчитать, как часто данная молекула сталкивается с другими. Знать частоту столкновений очень важно, в частности, для химической кинетики – науки, которая изучает скорость химических реакций.

Несмотря на то что молекулы воздуха все время «путаются под ногами» молекул йода (такое меткое выражение употребил лауреат Нобелевской премии по химии Николай Николаевич Семёнов), пары йода тем не менее распространяются все дальше от кристаллов. Это явление называется диффузией (слово происходит от лат. diffusio – «распространение», «растекание»). Быстрее всего диффузия происходит в газах, намного медленнее – в жидкостях, совсем медленно – в твердых телах.

Задача о диффузионном движении молекулы очень похожа на задачу о броуновском движении. В 1827 г. английский ботаник Роберт Броун, наблюдая в микроскоп за взвешенными в воде мельчайшими частицами (например, за зернами, выделенными из клеток пыльцы некоторых растений), неожиданно обнаружил, что эти частицы непрерывно совершают хаотические движения. И лишь много десятилетий спустя ученые поняли, что это явление связано с беспорядочными ударами невидимых молекул воды. Когда, наблюдая за частицами в микроскоп, на носили на клетчатой бумаге их положение через определенное время (например, каждые полминуты), получались ломаные линии – такие, как приведены на рисунке. Оказалось, что очень малые частицы подвержены со всех сторон непрерывным ударам молекул воды и эти удары не компенсируют друг друга (как в случае больших частиц). Если бы мы могли следить за положением данной молекулы в ходе ее непрерывных соударений с другими и нанесли эти положения на бумагу, то получилась бы такая же картинка.

Зарисовка последовательных положений трех броуновских частиц (капельки камеди размером около 1 мкм в эмульсии), сделанная французским физиком Жаном Перреном в 1908 г.

В этом хаосе движений смогли разобраться в начале ХХ в. Альберт Эйнштейн и польский физик Мариан Смолуховский, которые решили задачу о случайных блужданиях молекулы (или очень маленькой частицы). Сравнивая движения молекул и броуновских частиц, Смолуховский отмечал, что «частицы, взвешенные в жидкой или газообразной среде, ведут себя так, как если бы они были самостоятельными молекулами с нормальной кинетической энергией, но соответственно с гораздо меньшей длиной свободного пути». Остроумные физики вскоре обозвали случайные блуждания молекулы или броуновской частицы «прогулкой пьяницы» (по‑английски the drunkard’s walk), причем с помощью этой «модели» оказалось возможным легко и наглядно вывести основную формулу для диффузии. В такой необычной форме задача о случайных блужданиях звучит так. Поздно вечером из кабачка, расположенного в середине улицы (пункт 0), вышел подвыпивший моряк и направился… допустим, к ближайшей остановке; обе они находятся в нескольких сотнях метров по обе стороны от кабачка. Улица освещена фонарями на столбах, расстояние между которыми равно λ. Моряк не помнит, в какую сторону нужно идти от пункта 0, и выбирает направление произвольно. Дойдя до ближайшего фонаря, он немного отдыхает, ухватившись за столб, а потом идет дальше, до следующего фонаря, а так как он не помнит, откуда пришел, то может направиться в любую сторону с равной вероятностью. Спрашивается, дойдет ли он в конце концов до какой‑нибудь остановки или так и будет совершать колебания около начального пункта 0, то удаляясь ненамного от него, то опять приближаясь?

Решение этой строго научной задачи такое: постепенно моряк будет все дальше удаляться от начального пункта, хотя и значительно медленнее, чем если бы он двигался только в одну сторону. Это можно показать достаточно простым способом.

Нам нужно выразить расстояние S N от нулевой точки до местоположения моряка после N его блужданий от одного фонаря до другого, если известно среднее расстояние между столбами λ. (Отметим сразу, что для молекулы величина S соответствует диффузионному смещению – расстоянию, на которое продвинутся пары йода в воздухе или окрашенные ионы в воде; величина λ соответствует среднему свободному пробегу молекулы – расстоянию, которое она пролетает в свободном полете от одного столкновения до другого; величина N соответствует числу столкновений за определенное время – время, за которое диффузия прошла на расстояние S.)

А теперь немного простой математики. Дойдя до первого фонаря, моряк пройдет расстояние S 1 = ±λ: + λ, если он пошел вправо, и – λ, если пошел влево от точки 0. Но нам не важно, в какую сторону пошел моряк, а важно только, какое расстояние он прошел. Чтобы избавиться от знаков, возведем обе части этого равенства в квадрат: S 12 = λ2.

Пусть теперь, совершив N – 1 таких блужданий, моряк оказался на расстоянии S N –1 от начала. Пройдя до следующего фонаря, он очутится либо дальше, либо ближе к точке 0, т. е. S N = SN –1± λ.

Избавляемся от неопределенности в знаках таким способом. Возводим обе части равенства в квадрат: (S N)2 = (S N –1)2 ± 2λ S N –1 + λ2. Теперь представим себе, что моряк много раз совершил единичное блуждание от точки S N –1 к точке S N. В половине случаев, когда точка S N расположена дальше, чем точка S N –1, мы получим (S N)2 = (S N –1)2 + 2λ S N –1 + λ2, а в половине случаев, когда точка S N расположена ближе к началу, чем точка S N –1, мы получим (S N)2 = = (S N –1)2 – 2λ S N + λ2. Таким образом, плюсы и минусы взаимно сократятся, и в среднем квадрат удаления после N ‑го блуждания будет равен (S N)2 = (S N –1)2 + λ2.

Исходя из этой формулы и учитывая, что S 12 = λ2, получаем, что S 22 = S 12 + λ2 = 2λ2 (квадрат предыдущего значения плюс λ2), S 32 = = 3λ2 и т. д. То есть квадрат смещения после N ‑го блуждания (S N)2 = N λ2 или

.

Вот мы и получили основную формулу для процесса случайных блужданий. Из нее следует, например, что трезвый моряк, идущий все время в одном направлении, пройдя N = 100 столбов, расстояние между которыми λ = 20 м, удалится от точки 0 на 2000 м = 2 км. Подвыпивший же моряк удалится от начала всего на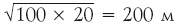

. Но все же в какую‑нибудь сторону удалится!

Другой пример. Многие, возможно, замечали, что шнур от телефонной трубки часто очень сильно закручен в одну сторону. Причина может быть та же: если много раз снимать трубку, а потом класть ее на рычаг, случайно повернув то в одну сторону, то в другую, то в конце концов трубка окажется много раз повернутой в какую‑нибудь одну сторону, и для распрямления провода его придется раскручивать.

Теория случайных блужданий имеет и более важное практическое приложение. Говорят, что без компаса и в отсутствие ориентиров (солнце, звезды, шум шоссе или железной дороги и т. п.) человек бродит в лесу, по полю в буране или в густом тумане кругами, все время возвращаясь на прежнее место. На самом деле он ходит не кругами, а примерно так, как движутся молекулы или броуновские частицы. На исходную точку он вернуться может, но только случайно. А вот свой путь он пересекает много раз – как броуновская частица на рисунке. Рассказывают также, что замерзших в пургу людей находили «в каком‑нибудь километре» от ближайшего жилья или дороги. Однако на самом деле у человека не было никаких шансов пройти этот километр, и вот почему.

Чтобы рассчитать, насколько сместится человек в результате случайных блужданий, надо знать ту самую величину λ; в данном случае это расстояние, которое человек может пройти по прямой, не имея никаких ориентиров. Эту величину с помощью студентов измерил профессор математики Московского государственного университета инженерной экологии Б. С. Горобец. Он, конечно, не оставлял их одних в дремучем лесу или на заснеженном поле, все было проще: студента ставили в центре пустого стадиона, завязывали ему глаза и просили в полной тишине (чтобы исключить ориентирование по звукам) пройти до конца футбольного поля. Оказалось, что в среднем студент проходил по прямой всего лишь около 20 м (когда отклонение от прямой не превышало 5°), а потом начинал все более отклоняться от первоначального направления. В конце концов он останавливался, далеко не дойдя до края.

Пусть теперь человек идет (вернее, блуждает) в лесу со скоростью 2 км/ч (для дороги это очень медленно, но для густого леса – очень быстро!), тогда если величина λ равна 20 м, то за час он пройдет 2 км, но сместится всего лишь на 200 м, за два часа – примерно на 280 м, за три часа – 350 м, за 4 часа – 400 м и т. д. А двигаясь по прямой с такой скоростью, человек за 4 часа прошел бы 8 км и, скорее всего, вышел бы если не к жилью, то к дороге, просеке, речке, высоковольтной линии. Поэтому в инструкциях по технике безопасности полевых работ есть такое правило: если ориентиры потеряны (сплошная облачность, не слышно шума шоссе или железной дороги), надо оставаться на месте, обустраивать убежище и ждать окончания ненастья (может выглянуть солнце) или помощи. В лесу же двигаться по прямой помогут ориентиры – деревья или кусты, причем каждый раз надо держаться двух таких ориентиров – одного спереди, другого сзади. Но, конечно, лучше всего брать с собой компас…

Вернемся теперь к молекулярной диффузии. Итак, молекула йода хаотично мечется между огромным количеством мешающих ей молекул воздуха, постепенно смещаясь все дальше – в соответствии с выведенной формулой. Скорость движения молекулы I2 при комнатной температуре равна, как мы помним, 170 м/с. В отсутствие столкновений (например, в глубоком вакууме космического пространства) эта молекула, двигаясь по прямой в одном направлении, прошла бы за время t расстояние L = ut. Это же расстояние можно получить, сложив все отрезки между столкновениями: L = λ N. Таким образом, ut = λ N. В случае же диффузии, при частых столкновениях, молекула сместится на значительно меньшее расстояние: S = λ√ N. Исключив из этих двух формул не очень интересное для нас значение N (ведь оно зависит от времени диффузии), получим очень важную формулу: S 2 = u λ t, или λ = = S 2/ ut. А частота столкновений равна Z = N / t = u /λ = u 2 t / S 2.

Формулы получены, настало время ими воспользоваться. Для этого нужен не очень сложный эксперимент. Поместим кристаллик йода на дно пробирки и поставим ее в теплую воду, чтобы ускорить диффузию. Эксперимент показывает, что при температуре 59 °С (332 К) за две минуты (120 с) пары йода поднялись примерно на 6 см. При этой температуре средняя скорость молекул йода равна 160 =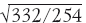

= 183 м/с. Таким образом, средний свободный пробег молекул I2 равен λ = S 2/(ut) = (0,06 м)2/(183 · 120) ≈ 1,6 · 10–7 м = 0,16 мкм – ничтожно малая величина! А вот частота столкновений получилась огромной: Z = u /λ = 183/1,6 · 10–7 ≈ ≈ 1,1 · 109, т. е. более миллиарда столкновений в секунду! С такой частотой сталкиваются между собой и молекулы воздуха. Двигаясь по прямой со скоростью 183 м/с, молекула йода за те же две минуты пролетела бы примерно 22 км!

Полученные значения для молекул йода не очень точны, так как массы молекул I2, O2 и N2 сильно отличаются (в 254/29 = = 8,8 раза), и в формулы для диффузии необходимо вводить поправки. Однако качественно проведенные расчеты дают правильный результат. Это можно подтвердить известными данными для диффузии. Например, для самодиффузии молекул кислорода в кислороде при нормальных условиях средний свободный пробег λ = 0,12 мкм – величина того же порядка, что и полученная для йода (0,16 мкм).

Средний свободный пробег молекул (и частота столкновений), конечно, сильно зависит от давления газа. Так, на высоте 10 км (примерно уровень самой высокой горы на Земле) давление воздуха снижается до 210 мм рт. ст., а средний свободный пробег молекул О2 и N2 увеличивается до 2 мкм, хотя и остается очень маленьким. На высоте 50 км (давление 0,76 мм рт. ст., т. е. в 1000 раз ниже нормального) λ = 0,08 мм, а на высоте 100 км (давление там снижается до 6 · 10–4 мм рт. ст.) λ = 9,5 см. Это уже хороший вакуум. При таком давлении электроны в кинескопе телевизора смогут почти свободно долетать до экрана, рисуя на нем изображение; если же вакуум в телевизионной трубке хоть немного нарушится, узкий электронный луч сильно «размажется» по дороге, сталкиваясь с молекулами воздуха, и никакого изображения не получится. В космосе в условиях высокого вакуума столкновений практически нет, и средний свободный пробег достигает многих тысяч километров.

Теперь попробуем оценить, через какое время мы почувствовали бы запах разлитых духов, если бы молекулы пахучего вещества распространялись в воздухе только за счет диффузии. Результат окажется удивительным. Действительно, молекулярная масса у многих пахучих веществ примерно такая же, как у молекул йода. В таком случае на расстояние S = 3 м эти молекулы диффундировали бы в течение времени t = S 2/ u λ = 9/183 ·1,6 ·10–7 ≈ 300 000 c = 85 часов! Понятно, что мы чувствуем запах намного быстрее в результате не диффузии, а потоков воздуха, т. е. конвекции.

До сих пор мы рассматривали диффузию в газах. В жидкостях она происходит намного медленнее. Например, смещение для ионов кобальта в водном растворе (эти ионы розового цвета) описывается формулой S 2 = Dt = 7,3 · 10–6 t см 2 /с (величина D называется коэффициентом диффузии, она получена экспериментально и аналогична произведению u λ в полученной ранее формуле). Поэтому, например, через 1000 с (около 17 мин) эти ионы пройдут в растворе всего лишь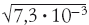

= 0,085 см ≈ 1 мм.

Диффузию в жидкостях легко наблюдать экспериментально. Проще всего это сделать для окрашенных ионов. Приготовим в небольшой баночке (например, из‑под пенициллина) раствор желатина такой концентрации, чтобы в холодильнике он превратился в студень (обычно достаточно приготовить 2–3%‑ный раствор в теплой воде, дождавшись полного растворения желатина после его набухания). С помощью маленького пинцета аккуратно поместим в центр баночки небольшой кристаллик хорошо растворимой в воде окрашенной соли, например медного купороса или перманганата калия. Через некоторое время вокруг кристаллика образуется окрашенный шарик, который медленно увеличивается в диаметре в результате диффузии ионов во всех направлениях от кристалла. Коллоидный раствор желатина практически не влияет на диффузию ионов в воде; его назначение – препятствовать конвективным потокам жидкости, которые неизбежно возникают в растворе, перемешивают его и смазывают картину. Правда, перманганат‑ионы могут реагировать с желатином, задубливая его, поэтому для количественных измерений надо использовать кристаллик инертного органического красителя, например бриллиантового зеленого. Но для качественной характеристики диффузии опыт с перманганатом калия весьма нагляден: с ним граница диффузии видна более четко. За день радиус шарика достигает примерно 0,8 см.

Можно поступить и иначе: поместить кристаллик перманганата калия на дно узкой трубочки, запаянной с одного конца, и с помощью шприца с тонкой иглой осторожно наполнить трубочку водой. За диффузией в этом случае следят по перемещению окрашенной границы между раствором и чистой водой (в узкой трубке конвективные потоки жидкости затруднены).

Дата добавления: 2014-11-25