Методичні рекомендації до самостійної роботи. Тема 6. Логічні основи теорії аргументації

План вивчення теми

Тема 6. Логічні основи теорії аргументації

Бібліографічний список

Основна література (1), (2), (6), (8), (10)

Додаткова література (1), (3)

Мета: Засвоїти що таке аргументація і доведення, критика і спростування. Стратегія і тактика аргументації та критики. Правила аргументації і критики, доведення і спростування. Правила по відношенню до тези, можливі помилки. Правила по відношенню до аргументів, можливі помилки. Правила і помилки по відношенню до форми аргументації і критики.

1. Аргументація і доведення.

2. Критика і спростування.

3. Стратегія і тактика аргументації та критики. Правила аргументації і критики, доведення і спростування.

4. Правила по відношенню до тези, можливі помилки. Правила по відношенню до аргументів, можливі помилки. Правила і помилки по відношенню до форми аргументації і критики.

Соціально-політичному життю людей притаманна поліфонія думок, поглядів, точок зору і т.д., яка є своєрідним свідченням культурного плюралізму. І все ж, заради певних цілей і потреб, людині необхідно намагатися усувати відмінність у поглядах. Таких ситуацій безліч: наукові конференції, судові засідання, слухання в парламенті, переговори з приводу політичних, економічних проблем, не кажучи вже про ситуації повсякденного життя.

Для позначення процесу обміну протилежними думками часто використовують слово “суперечка”. Саме у ситуаціях суперечок найчастіше застосовуються процедури доведення і спростування, аргументації і критики. Побіжно охарактеризуємо деякі форми суперечок.

Дискусія – найчастіше, наукова суперечка двох або декількох людей, під час якої з'ясовують і зіставляють різні точки зору з метою пошуку правильного вирішення спірного питання, або ж з метою пошуку істини чи, принаймні, наближення до неї.

Під диспутом сьогодні розуміється публічна суперечка двох людей з приводу наукового або суспільно важливого питання. Слово “дебати” найчастіше застосовують у політичній сфері (наприклад, “парламентські дебати”). Часто цим словом позначають суперечки, що виникають під час обговорення доповідей, виступів на зборах, засіданнях, конференціях і т.д.

Перебуваючи в стані суперечки, люди керуються різними методами і переслідують різні цілі. Тому можна говорити про:

а) суперечку заради істини (тобто діалектичну суперечку, де слову “діалектика” надають його первісного значення, а саме, “мистецтво досягнення істини в бесіді”);

б) суперечку, мета якої – просто переконати іншу людину;

в) суперечку заради перемоги в суперечці, тобто “еристичну” суперечку. Її мета – взяти гору над “супротивником” за будь-яку ціну, використовуючи будь-які методи. В еристичній суперечці керуються різними мотивами, перемога може бути потрібною для демонстрації своєї принциповості або для свого самоствердження. Отже, еристика (від грець, еns – суперечка) – це мистецтво проведення суперечки.

Сторони, які сперечаються, називаються, відповідно, пропонентом і опонентом.

Пропонент, або протагоніст – той, хто висуває, обстоює деяку тезу.

Опонент, або антагоніст – той, хто заперечує.

Зазначимо, що не будь-яку ситуацію суперечки (тобто ситуацію обміну протилежними думками і намагання усунути розходження у поглядах) характеризують як аргументативну дискусію.

Аргументативна дискусія – це така форма суперечки, яка здатна зробити внесок в інтелектуальний прогрес. Вона відбувається переважно на платформі розуму з використанням раціональних засобів обґрунтування.

У найширшому значенні термін “аргументація” вживається для позначення процесів обстоювання пропонентом деякого твердження з метою доведення того, що це твердження є істинним, слушним.

Поруч із терміном “аргументація” нерідко використовують термін “доведення”.

Доведення (на відміну від аргументації) – це логічна операція обґрунтування істинності одного твердження (судження, гіпотези, концепції) за допомогою інших істинних і зв'язаних з ним суджень шляхом побудови відповідного міркування.

Доведення – це завжди правильне міркування, в якому відношення між засновками і висновком є відношенням логічного слідування (такі міркування називаються демонстративними).

Доведення є окремим (особливим) випадком аргументації, позаяк аргументація може здійснюватися не обов'язково за допомогою логічно бездоганних міркувань та істинних аргументів. Аргументація не буде доведенням або у випадку використання лише правдоподібних (недостовірних) аргументів, або у випадку недемонстративних міркувань.

Доказовість – це логічна риса мислення, а переконливість – психологічна риса, що ґрунтується на логічній і фактичній достовірності.

Доведення здійснюється у формі умовиводу або системи умовиводів, елементами якої можуть бути умовиводи різних форм і видів.

Структурними елементами доведення є:

• теза;

• аргументи (підстава, докази);

• демонстрація (форма зв'язку тези і аргументів).

Теза (Т) – положення, істинність якого треба довести. Логічною формою вираження тези є висловлювання (судження). За умов, коли теза формулюється не лише для доведення її істинності, а й для акцентування уваги на даній проблемі, вона може набирати форму запитання. Наприклад, тезу можна сформулювати так: “Чи здійснюються ринкові перетворення в Україні?” У цьому випадку, щоб довести істинність позитивної відповідь на це питання: “Так, в економіці України здійснюються ринкові перетворення”, треба навести аргументи, які підтвердять істинність висунутої тези.

Аргументи (лат. аrgumentum – основа, доказ) – це вихідні теоретичні і фактичні положення, які є достатньою підставою для підтвердження. істинності тези. Суть доведення саме і полягає в обґрунтуванні істинності тези за допомогою аргументів. Аргументами при доведенні можуть бути: факти, закони, теорії, аксіоми, постулати, визначення тощо, тобто положення, істинність яких вважається безумовною.

Факт – (лат. factum – те, що відбулося) – це реальна подія, яка існує зараз або мала місце у минулому.

Закон – це об'єктивний, сталий, внутрішній, необхідний, істотний зв'язок, загальний для даної групи явищ, який повторюється за однакових умов і веде у цих умовах до певного результату.

Теорія (грецьк. – розгляд, дослідження) – це форма достовірного наукового знання, підтвердженого практикою. Це система суджень, пов'язаних між собою способами залежності, доведення або виведення одних знань з інших.

Аксіома – судження, істинність якого не потребує доведення в межах даної дедуктивної теорії і відіграє роль вихідного положення і аргументу для обґрунтування істинності інших її положень.

Постулат (лат. postulatum – вимога) – положення, переконливе припущення, яке вводиться у систему доведення у межах даної теорії без доказу і вважається достатньою підставою для обґрунтування істинності інших положень.

Вихідні основи кожної науки – судження про достовірні окремі факти, аксіоми, закони, постулати і визначення – називаються безпосередніми основами доведення. Положення, що формулюються на цій основі, називаються похідними положеннями доведення.

Демонстрація – логічне міркування, у процесі якого з аргументів із логічною необхідністю виводиться істинність чи хибність тези.

Демонстрація на основі певної сукупності логічних правил показує послідовність логічного зв'язку тези з її аргументами та правомірність обґрунтованості її істинності (хибності). Вона постає однією із форм умовного зв'язку. Так, аргументи (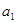, ,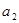..., 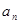) виконують функцію підстави доведення, а теза (Т) є їх логічним наслідком. У такому випадку логічна схема доведення буде мати вигляд:

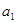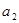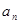(, ,..., )→Т.

Логічний перехід від аргументів до тези відбувається у формі умовиводу (або їх низки). Це означає, що обґрунтування тези може приймати форму дедуктивних, індуктивних умовиводів або умовиводу за аналогією (або їх комбінації).

У залежності від способу аргументації істинності тези доведення поділяються на прямі та непрямі.

Прямим називається доведення, в якому істинність тези доведення безпосередньо випливає з аргументів.

Якщо відомо, що аргументи істинні і з них безпосередньо випливає теза, то вона теж істинна. За цих обставин доведення є ланцюгом (послідовністю) суджень, пов'язаних відношенням логічного спілкування. Виражається ця послідовність у формі імплікації А→В (де А – антецедент (умова), а В – висновок або ствердження).

Найчастіше доведення здійснюються за такою схемою:

1) вводиться доводжуване речення у формі допущення (доведення);

2) з наявних речень, до яких можна приєднати раніше встановлені істини (аксіоми, постулати, закони тощо), виводиться наслідок;

3) доведення закінчується здобуттям висновку (доводжуваного висловлювання).

Доведення підлягає двом видам правил:

а) правила побудови доведення, які визначають структуру можливого доведення і підказують його “ідею”;

б) правила логічного слідування, тобто правила, за якими з уже наявних суджень виводять, як наслідок, нові судження.

Цими правилами можуть бути: М – П (modus ponens), УК (усунення кон'юнкції), ВК (введення кон'юнкції), УД (усунення диз'юнкції), ВД (введення диз'юнкції) та ін. Наприклад, припустимо, що треба довести форму.

((А→В) (В→С))→(А→С)

Праворуч від доведення будемо записувати правила, якими користуватимемося при доведенні. Доведення вважають закінченим, якщо кінцева формула доведення збігається з формулою висновку.

При доведенні ми керуємося такими правилами: будь-який крок доведення ми можемо записати як:

1) одну з формул засновників А→В, В→С, А→С (як допущення);

2) формулу, доведення якої невідоме;

3) формулу, що раніше випливає з раніш написаних формул, за одним з правил МП, УК, ВК, УД, ВД.

Доведення:

1. (А→В) (В→С)	– допущення (засновки).
2. (А→В)	– УК із 1.
3. А	– допущення (антецедент формули А→С).
4. В	– МП із 2 і 3.
5. В→С	– УК із 1.
6. С	– МП із 5 і 4.

Так, послідовним висуванням шести формул, доведення яких записано за правилами слідування, ми довели істинність формули:

((А→В) (В→С))→(А→С)

Проте в деяких випадках пряме доведення неможливе. Саме тоді звертаються до непрямого доведення.

Непряме доведення – таке доведення, в якому істинність тези (Т) обґрунтовується шляхом доведення хибності антитези (-Т). В даному випадку, на підставі закону виключеного третього, хибність антитези дає змогу говорити про істинність доводжуваної тези.

Антитеза – це судження (висловлювання) суперечне тезі. Вона може бути записана однією з наступних форм:

• якщо теза – це Т, то антитезою буде - (-Т);

• якщо тезою у розділовому судженні АÚВÚС маємо А, то антитезою будуть В і С.

Залежно від типу антитези непряме доведення поділяють на два види:

• апагогічне;

• розділи.

(Слово „апагогічне” походить від грецьк. – „той, що відводить”).

Хід міркування в апагогічній аргументації виконують у три етапи:

I етап: для обґрунтування деякої тези (Т) спочатку формують її антитезу - (-Т) і припускають істинність цієї антитези.

II етап: логічно виведені із (-Т) наслідки співставляють з положеннями, істинність яких установлена (С). Якщо наслідки є несумісними з цими даними, то вони розцінюються як хибні (-С). Потім із хибності наслідків по modus toliens виводимо хибність допущення, тобто антитези (-Т). Схема міркування:

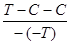
ІІІ етап: із хибності допущення (-Т) на підставі закону виключення третього (або на підставі хибності антитези, тобто (-(-Т)) випливає висновок щодо істинності тези (Т). Схема міркування:

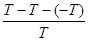Такий спосіб демонстрації хибності деякого припущення (у нашому випадку антитези (-Т), шляхом виведення з нього суперечності) називають приведенням до абсурду.

Продемонструємо аналогічне доведення з використанням мови символів і відповідних правил логічного слідування.

Наприклад, треба довести формулу: ((АÙ(–В)®В)®(А®В). При доведенні будемо керуватися такими правилами:

1. Одну з формул ((АÙ(–В)®В)®(А®В) можемо записати на будь-якому кроці доведення (як припущення).

2. Можемо написати формулу загального висновку (як припущення зворотного доведення).

3. Написати формулу, доведення якої раніше побудоване.

4. Записати формулу, що слідує з попередньо написаних формул, за одним з правил: МП, УК, ВК, УД, ВД.

Доведення:

1. (А®В)®В – вводимо допущення

2. А

3. (–В) – допущення зворотного доведення

4. А, (–В) – ВК із 2 і З

5. В – МП із 1 і 4

Суперечність 3 і 5.

Оскільки в процесі послідовного запису формул відповідно до правил слідування ми дістали дві суперечливі формули (–В) (3) і В (5), доведення вважається закінченим. Припустивши (–В) (3), тобто істинність антитези, ми прийшли до абсурду, це означає істинність.

У розділовому непрямому доведенні теза, що доводиться, є членом розділового судження, члени якого повинні вичерпувати всі можливі допущення і виключати один одного. Доведення у цьому випадку полягає у спростуванні всіх припущень, один одного, яке и буде доводжуваною тезою.

Доведення здійснюється у формі модусу tollendo ponens розділового силогізму:

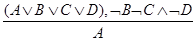
Гарантією істинності тези у розділовому непрямому доведенні є вичерпний перелік усіх можливих допущень, що виключають одне одного. Застосування механізму непрямого доведення пов'язане з певними труднощами. Під час такої аргументації необхідно тимчасово відхилятись від власне тези і залучати додатковий „матеріал”, додаткову інформацію, зосереджуючись на хибних твердженнях. Це, безперечно, ускладнює процес аргументативного міркування в цілому.

Дата добавления: 2014-11-25