Дополнительный код

Арифметика в двоичном коде

Практическая работа №1

1. Преобразовать в десятичный код следующие двоичные числа.

a) 0001₂

b) 0101₂

c) 1111₂

d) 0011110₂

e) 10000000₂

2. Преобразовать в двоичный код следующие десятичные числа

a) 23₁₀

b) 39₁₀

c) 55₁₀

d) 48₁₀

e) 113₁₀

3. Записать следующие восьмеричные числа в двоичном коде

a) 3₈

b) 152₈

c) 7642₈

d) 1036₈

e) 2105₈

4. Записать следующие шестнадцатеричные числа в двоичном коде

a) C₁₆

b) 6₁₆

c) CAB

d) 8B₁₆

e) 127₁₆

5. Записать сл. двоично-десятичные числа в десятичном коде

a) 0000 0001_DDK

b) 1000 0000_DDK

c) 0111 0110 0011_DDK

d) 0011 1001 1000_DDK

e) 0010 0000 0011 0101

6. Перевести десятичное число в двоичное с промежуточным переводом в восьмеричную и шестнадцатеричную системы счисления.

а) 1972₁₀ → A₈ → A₂

b) 1972₁₀ → A₁₆ → A₂

C двоичными числами, как и c десятичными, можно совершать арифметические операции.

Двоичное сложение выполняется по тем же правилам, как и десятичное, только перенос в следующий разряд производится после того, как сумма достигнет 2, а не 10. Два двоичных разряда складываются по следующему правилу:

А	В	А+В
		0 и 1 переноса

Сложение двоичных чисел в компьютере выполняется в специальном устройстве- сумматоре.

Двоичные числа можно вычитать так же как и десятичные, но в компьютере для операции вычитания также используется сумматор, который вычитание заменяет на сложение с отрицательным числом.

Например, 5-3=5+(-3)=2

Чтобы использовать число со знаком применяется дополнительный код числа.

Чтобы заменить операцию вычитания на операцию сложения, используется прямой, обратный и дополнительный коды, которые называются машинными кодами.

Прямой код — это положительное число.

Обратный код получают заменой единиц нулями, а нули единицами в прямом коде.

Чтобы получить дополнительный код числа, нужно сначала получить обратный код, затем к полученному обратному коду к младшему биту прибавить единицу.

Например:

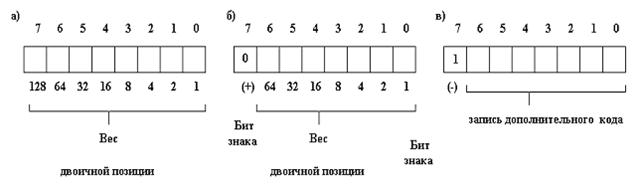
На рисунке а) дано обычное изображение 8-ми разрядного регистра микропроцессора или ячейки памяти.

На рисунке б) и в) показаны типовые 8-ми разрядные регистры для размещения чисел со знаком. Бит 7 является знаковым, то есть он указывает, является ли число положительным или отрицательным. При нуле в знаковом бите — число положительное; при единице в знаковом бите — число отрицательное.

Например:

Чтобы определить десятичное число двоичного числа, записанного в форме дополнительного кода, необходимо перевести его в прямой код. Для этого нужно заменить нули единицами, а единицы нулями, получить обратный код, затем к младшему биту прибавить единицу, полученное двоичное число преобразовать в десятичное, но взять с отрицательным знаком.

Например:

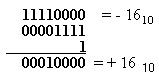
Задание. Определить являются ли числа положительными или отрицательными и дать их десятичные эквиваленты:

а) 01110000₂

б) 11001111₂

Дата добавления: 2014-11-09