Умножение и деление двоичных чисел

Арифметика в дополнительном коде

Микропроцессор может использовать число в дополнительном коде, так как может выполнять следующие операции: инверсию; инкрементирование (добавления 1 к числу) и сложение двоичных чисел.

Для того чтобы сложить десятичные числа (+7) и (-3), необходимо их перевести в двоичный код, дополнив их до 8 разрядов незначащими нулями слева, затем отрицательные числа взять в дополнительном коде и произвести сложение:

Например,

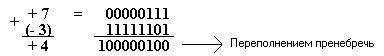
Переполнение означает, что для записи числа отведено недостаточное количество разрядов, произошло переполнение разрядной сетки. В данном случае переполнением пренебрегают.

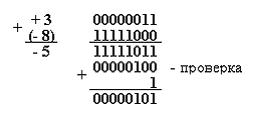
Сложить следующие десятичные числа с последующей проверкой:

Пример

Задание

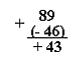
Умножение и деление двоичных чисел производится путем сдвига цифр соответственно влево или вправо и сложения.

Например:

При умножении чисел 1101 и 101

Множимое * 1101

Множитель 101

Первое частичное произведение 1101

Второе частичное произведение 0000

Третье частичное произведение 1101

Конечное произведение 1000001

Следует обратить внимание на то, что частичные произведения либо равны множимому, либо равны нулю (0). Из этого следует, что процедуру умножения можно сократить, если сложить множимое с самим собой столько раз, сколько единиц в множителе, при этом множимое записывается со сдвигом влево таким образом, чтобы самая правая цифра множимого находилась под единицей множителя.

Таким образом, в микропроцессоре операция двоичного умножения выполняется методом, получившим название “умножение путем сдвига и сложения”.

Операция деления, как и в десятичной арифметике, является обратной операции умножения и тоже приводится к последовательности операций сдвига и сложения.

Например:

Дата добавления: 2014-11-09