Линейная алгебра

Методические указания

Кривые второго порядка на плоскости

1. Какие кривые называют кривыми второго порядка?

2. Сформулируйте определение окружности, эллипса, гиперболы, параболы.

3. Напишите каноническое уравнение окружности, эллипса, гиперболы, параболы.

4. Сформулируйте свойства окружности, эллипса, гиперболы, параболы.

Пример Пусть дана система линейных уравнений 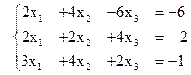(1).

(1)

Требуется найти решение этой системы методом полного исключения.

Запишем эту систему в виде прямоугольной таблицы, у которой в столбцах расположены коэффициенты при неизвестных, а в последнем столбце - свободные члены (после того, как их перенесли в правую часть уравнений). Эту таблицу будем называть "расширенная матрица системы".

Расширенная матрица этой системы имеет вид (2) .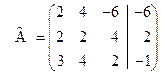

Первый шаг решения (I шаг) состоит в следующем.

1. Выбираем строку, у которой первый элемент не равен нулю (в нашем примере можно взять, например, первую строку). Эту строку назовем «разрешающая (ведущая) строка первого шага». Первый столбец назовем «разрешающий (ведущий) столбец первого шага», а элемент, расположенный на пересечении разрешающей строки и разрешающего столбца назовем «разрешающий (ведущий) элемент первого шага». Эта операция соответствует перемене местами уравнений системы, поэтому новая система будет равносильна исходной.

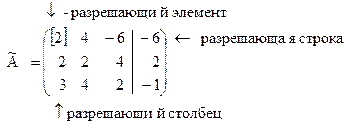
2. Разрешающую (первую) строку делим на разрешающий элемент. Получаем новую строку (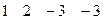), которую записываем первой строкой в новой матрице 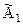. При этом первая строка новой матрицы матрица примет вид:

.

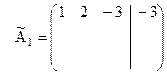3. Чтобы найти вторую строку матрицы 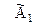,ко второй строке матрицы 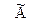прибавим новую первую строку из матрицы 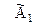, предварительно умножив ее на такое число, чтобы в первом столбце оказался ноль. В нашем примере ко второй строке матрицы 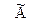нужно прибавить первую строку матрицы 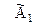, умноженную на (-2), получим: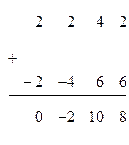

Теперь матрица 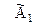будет иметь вид:

.

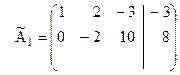4. Чтобы найти третью строку матрицы 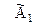,к третьей строке матрицы 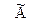прибавим новую первую строку из матрицы 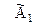, предварительно умножив ее на такое число, чтобы в первом столбце оказался ноль. В нашем примере ко второй строке матрицы 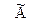нужно прибавить первую строку матрицы 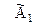, умноженную на (-3), получим: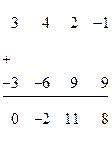

Теперь матрица 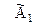будет иметь вид:

.

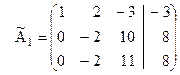Если матрицу 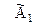будем рассматривать, как систему уравнений, то увидим, что в результате элементарных преобразований получили систему равносильную исходной, причем неизвестная 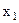в первое уравнение входит с коэффициентом единица, а из остальных уравнений она исключена.

Второй шаг решения (II шаг) состоит в том, что неизвестная 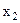исключается из всех уравнений кроме второго, а во второе должна входить с коэффициентом единица.

1. Выбираем любую строку, которая еще не была разрешающей, и у которой второй элемент не равен нулю (в нашем примере можно взять, например, вторую строку матрицы 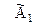). Эту строку назовем «разрешающая (ведущая) строка второго шага». Второй столбец назовем «разрешающий (ведущий) столбец второго шага», а элемент, расположенный на пересечении разрешающей строки и разрешающего столбца назовем «разрешающий (ведущий) элемент второго шага».

.

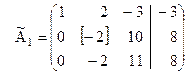2. Разрешающую (вторую) строку делим на разрешающий элемент. Получаем новую строку (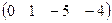), которую записываем второй строкой в новой матрице 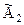. При этом новая матрица примет вид:

.

3. Чтобы найти первую строку матрицы 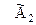,ко второй строке матрицы 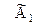прибавим новую вторую строку из матрицы 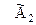, предварительно умножив ее на такое число, чтобы во втором столбце оказался ноль. В нашем примере к первой строке матрицы 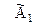нужно прибавить вторую строку матрицы 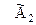, умноженную на (-2), получим: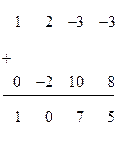

Теперь матрица 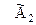будет иметь вид:

.

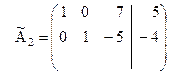4. Чтобы найти третью строку матрицы 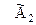, к третьей строке матрицы 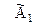прибавим новую вторую строку из матрицы 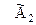, предварительно умножив ее на такое число, чтобы во

втором столбце оказался ноль. В нашем примере к третьей строке матрицы 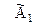нужно прибавить вторую строку матрицы 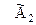, умноженную на (+2), получим: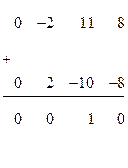

Теперь матрица 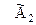будет иметь вид:

.

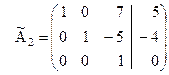Если матрицу 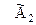рассматривать, как систему уравнений, то увидим, что в результате элементарных преобразований получили систему равносильную исходной, причем неизвестная

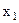исключена из всех уравнений кроме первого а 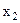из всех уравнений кроме второго.

Третий шаг решения (III шаг) состоит в том, что неизвестная 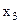исключается из всех уравнений кроме третьего, а в третье должна входить с коэффициентом единица.

.

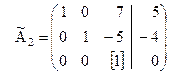Следовательно, на третьем шаге третья строка и третий столбец будут разрешающими, а разрешающий элемент оказался равным единице. Поэтому третий шаг сразу можно начать с исключения 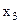из всех уравнений кроме разрешающего. В нашем примере нужно к первой строке прибавить разрешающую, умноженную на (-7), а ко второй прибавить разрешающую строку, взятую с коэффициентом (5). В результате получим новую матрицу:

.

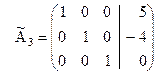Если заменить эту матрицу соответствующей ей системой уравнений, то получим ответ:

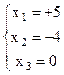
Обобщив все проведенные в примере вычисления, можно сформулировать в общем виде алгоритм любого (к - го) шага.

Алгоритм к – го шага.

(1) Выбираем к – ую разрешающую строку среди тех строк, которые еще не были разрешающими и у которых на к – ом месте стоит элемент отличный от нуля. При этом к – ый столбец будет разрешающим столбцом, а элемент стоящий на их пересечении – разрешающим элементом.

(2) Разрешающую строку делим на разрешающий элемент и записываем на к – ое место в новой матрице.

(3) Ко всем остальным строкам матрицы, полученной на предыдущем шаге, прибавляем строку, полученную в (2) и взятую с таким коэффициентом, чтобы в к – ом столбце новой матрицы все элементы кроме к – го оказались нулями.

Примечания

1. Если в процессе вычислений появятся несколько одинаковых строк, то все кроме одной нужно отбросить.

2. Если в процессе решения появится нулевая строка, то ее нужно отбросить.

3. Все элементы любой строки можно умножать или делить на число отличное от нуля.

4. Если в строке только последний элемент отличен от нуля, то система противоречива

и решений не имеет.

5. Если на последнем шаге оказывается, что количество неизвестных больше, чем

количество уравнений, то система имеет бесчисленное множество решений.

Пример Система трёх линейных уравнений с тремя неизвестными х₁, х₂, х₃

задана расширенной матрицей .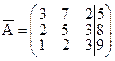

Требуется:

1) записать систему в канонической форме (в виде системы уравнений),

2) решить эту систему по формулам Крамера, причём определители вычислять,

используя их свойства.

Дата добавления: 2014-11-25