
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Здесь коэффициенты с верхним индексом (1) получены после 1-ого шага
|
|
|
|
Недостаток формул Крамера и метода обратной матрицы- их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных задач.
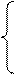 Пример. Решить по формулам Крамера и методом обратной матрицы следующую систему уравнений:
Пример. Решить по формулам Крамера и методом обратной матрицы следующую систему уравнений:
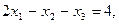
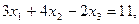
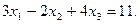
Для применения формул Крамера вычислим определитель системы:
 |  |
2 -1 -1
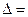 3 4 -2 = 60
3 4 -2 = 60
3 -2 4
Заменим в определителе системы первый столбец на столбец свободных членов, вычислим полученный определитель:
 |  |
4 -1 -1
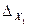 = 11 4 -2 =180
= 11 4 -2 =180
11 -2 4
Заменим в определителе системы второй столбец на столбец свободных членов, вычислим полученный определитель:

 2 4 -1
2 4 -1
3 11 -2
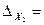 3 11 4 =60
3 11 4 =60
Заменим в определителе системы третий столбец на столбец свободных членов, вычислим полученный определитель:
 |  |
2 -1 4
3 4 11
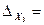 3 -2 11 =60.
3 -2 11 =60.
Вычислим значения неизвестных:
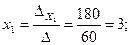
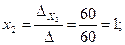
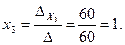
Для применения метода обратной матрицы представим систему уравнений в матричной форме:





 2 -1 -1
2 -1 -1 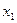 4
4
3 4 -2 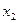 = 11
= 11
3 -2 4 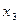 11
11
Далее рассчитываем обратную матрицу:
 |  |
12 6 6
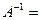
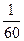 -18 11 1
-18 11 1
-18 1 11
По формуле (4) получаем решение:






12 6 6 4 3
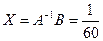 -18 11 1 11 = 1
-18 11 1 11 = 1
-18 1 11 11 1
Метод Гаусса
Метод Гаусса - метод последовательного исключения неизвестных- заключается в том, что с помощью элементарных преобразований система уравнений приводиться к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные.
Предположим, что в системе (1) 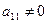 (этого всегда можно добиться перестановкой уравнений)
(этого всегда можно добиться перестановкой уравнений)
Шаг 1. Умножим 1-ое уравнение на 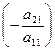 и прибавим ко второму; затем умножим 1-ое уравнение на
и прибавим ко второму; затем умножим 1-ое уравнение на 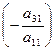 и прибавим к третьему, и т.д., и, наконец, умножим 1-ое уравнение на
и прибавим к третьему, и т.д., и, наконец, умножим 1-ое уравнение на 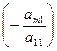 и прибавим к m-му уравнению. Получим преобразованную систему уравнений, в которой
и прибавим к m-му уравнению. Получим преобразованную систему уравнений, в которой 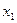 исключено из всех уравнений, кроме первого:
исключено из всех уравнений, кроме первого:
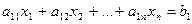
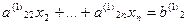
……………………….. (6)
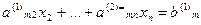
Шаг 2. Предположим, что 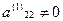 .(этого всегда можно добиться перестановкой уравнений с перенумерацией).
.(этого всегда можно добиться перестановкой уравнений с перенумерацией).





 Умножаем 2-ое уравнение на числа -
Умножаем 2-ое уравнение на числа - 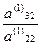 ,
, 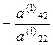 , …,
, …, 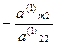 и прибавим полученные уравнения соответственно к третьему, четвертому,
и прибавим полученные уравнения соответственно к третьему, четвертому,
…,m-му уравнению системы (6), исключая  из всех уравнений, начиная с третьего.
из всех уравнений, начиная с третьего.
Продолжая процесс последовательного исключения переменных, после (r-1)- го шага получим систему:
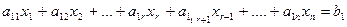
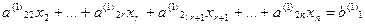
………………………………….
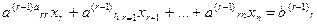 (7)
(7)
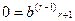
…………
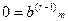
Если хотя бы одно из чисел 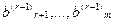 не равно нулю, то соответствущее равенство противоречиво, и система (1) несовместна. Для любой совместной системы (m-r) уравнений в системе (7) являются тождествами, и их можно не принимать во внимание при решении системы (1). После отбрасывания «лишних» уравнений возможны два случая:
не равно нулю, то соответствущее равенство противоречиво, и система (1) несовместна. Для любой совместной системы (m-r) уравнений в системе (7) являются тождествами, и их можно не принимать во внимание при решении системы (1). После отбрасывания «лишних» уравнений возможны два случая:
А) r=n, и в этом случае система (7) имеет треугольный вид;
Б) r<n, и система (7) имеет ступенчатый вид.
Переход системы (1) к равносильной системе (7) называется прямым ходом метода Гаусса, а нахождение переменных из системы (7)- обратным ходом.
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей системы (1), в которую, кроме матрицы А, дополнительно включен столбец свободных членов.
Пример. Решить методом Гаусса систему уравнений:
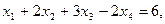
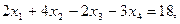
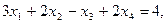
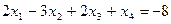
Расширенная матрица системы имеет вид:


 1 2 3 -2 6
1 2 3 -2 6
2 4 -2 -3 18
3 2 -1 2 4
2 –3 2 1 -8



 Теперь все действия над уравнениями будут эквивалентны действиям над строками матрицы. Умножаем 1-ую строку на -
Теперь все действия над уравнениями будут эквивалентны действиям над строками матрицы. Умножаем 1-ую строку на - 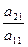 , т.е. на -
, т.е. на -  = -2, получаем
= -2, получаем
(-2 -4 -6 4 -12)
эту строку прибавляем ко второй строке, получаем новую 2-ю строку:
(0 0 -8 1 6).
Аналогично умножим 1-ую строку на (-3) и сложим с третьей строкой; умножим 1-ую строку на (-2) и сложим с 4-ой строкой. Расширенная матрица после 1-ого шага имеет вид:
1 

 2 3 -2 6
2 3 -2 6
0 0 -8 1 6
0 -4 -10 8 -14
0 -7 -4 5 -20
Первая строка при преобразованиях Гаусса остается без изменений. Для дальнейшего хода необходимо переставить 2-ую и 3-ю строки,чтобы 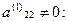
 |  |  |
1 2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 -7 -4 5 -20
На 2-ом шаге, поскольку 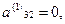 требуется только обнулить элемент
требуется только обнулить элемент 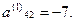 Для этого 2-ое уравнение умножим на
Для этого 2-ое уравнение умножим на 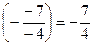 и сложим с 4-м уравнением. 2-ое уравнение после умножения выглядит так:
и сложим с 4-м уравнением. 2-ое уравнение после умножения выглядит так:
(0 7 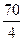 -
- 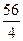
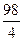 )
)
После 2-го шага матрица имеет вид:


 1 2 3 -2 6
1 2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 54/4 -36/4 -18/4
Поскольку в элементах последней строки одинаковый знаменатель, исключаем его; кроме того, можно сократить всю 4-ую строку на общий множитель 18:


 1 2 3 -2 6
1 2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 3 -2 1

 На 3-м шаге исключаем
На 3-м шаге исключаем 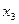 из 4-ого уравнения; для этого умножим 3-ю строку на 3/8 и сложим с 4-ой строкой:
из 4-ого уравнения; для этого умножим 3-ю строку на 3/8 и сложим с 4-ой строкой:
 1 2 3 -2 6
1 2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 0 -13/8 26
Теперь матрица системы имеет треугольный вид: все элементы ниже главной диагонали равны нулю.
Далее совершаем обратный ход метода Гаусса. 4-ое уравнение системы можно записать так:
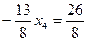
оно имеет решение: 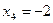 .
.
Подставляем полученное значение в 3-е уравнение:
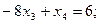
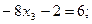
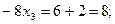
Теперь в 3-м уравнении только одно неизвестное 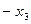 .Решаем уравнение, получаем
.Решаем уравнение, получаем 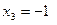 . Далее подставим известные
. Далее подставим известные 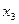 и
и 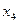 во второе уравнение:
во второе уравнение:
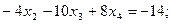
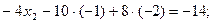
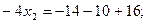
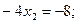
Отсюда 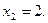
Подставляем в 1-ое уравнение известные 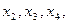 получаем решение:
получаем решение:
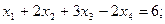
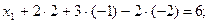
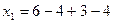
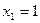
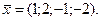
Вопросы для самоконтроля:
1. Чем отличается СЛАУ от систем произвольных уравнений?
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 553; Нарушение авторских прав?; Мы поможем в написании вашей работы!