
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Запишите условие параллельности и перпендикулярности прямых
|
|
|
|
Запишите различные виды уравнения прямой на плоскости и в пространстве.
ПРИМЕРНЫЕ ТЕСТЫ
| Вопрос | Варианты ответа | |
| I.Матрицы и определители | ||
| Сложение матриц А и В возможно только тогда, когда: | А и В имеют одинаковое количество строк и одинаковое количество столбцов | |
| обе матрицы квадратные | ||
| число столбцов матрицы А равно числу строк матрицы В | ||
| число строк матрицы А равно числу столбцов матрицы В | ||
| Умножение матрицы А на матрицу В возможно только тогда, когда: | число столбцов матрицы А равно числу строк матрицы В | |
| число строк матрицы А равно числу столбцов матрицы В | ||
| А и В имеют одинаковую размерность | ||
| обе матрицы квадратные | ||
| Диагональной называется матрица: | квадратная произвольного порядка, у которой все элементы равны нулю, кроме элементов на главной диагонали | |
| квадратная произвольного порядка, у которой на главной диагонали стоят единицы, а все остальные элементы нули | ||
| состоящая из нулей, кроме элементов на главной диагонали | ||
| состоящая из нулей, кроме элементов на главной диагонали, состоящей из единиц | ||
| II.Системы линейных уравнений и векторная алгебра | ||
| Теорема Кронекера - Капелли формулируется так: | система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы | |
| система линейных уравнений имеет единственное решение, если ранг матрицы совместной системы равен числу неизвестных | ||
| если ранг матрицы системы меньше числа неизвестных, то система линейных уравнений имеет бесконечное множество решений | ||
| система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы меньше ранга расширенной матрицы этой системы | ||
| Система линейных уравнений называется неопределенной, если она: | имеет более одного решения | |
| не имеет решений | ||
| является несовместной | ||
| имеет единственное решение | ||
| Несовместная система линейных уравнений: | не имеет решений | |
| имеет более одного решения | ||
| имеет не более одного решения | ||
| имеет единственное решение | ||
| Свободными называются переменные системы линейных уравнений, которые: | не являются базисными | |
| в данной системе образуют определитель, не равный нулю | ||
| в данной системе образуют определитель, равный нулю | ||
| являются в этой системе линейно зависимыми | ||
| III. Аналитическая геометрия | ||
| Уравнение прямой, проходящей через 2 точки, имеет вид: | (y-y1)/(y2-y1)=(x-x1)/(x2-x1) | |
| x/a+y/b=1 | ||
| y=kx+b | ||
| Ax+By+C=0 | ||
| Уравнение прямой в отрезках, отсекаемых на осях координат, имеет вид: | x/a+y/b=1 | |
| (y-y1)/(y2-y1)=(x-x1)/(x2-x1) | ||
| y=kx+b | ||
| Ax+By+C=0 | ||
| Нормальное уравнение окружности с центром в начале координат имеет вид: | 
| |
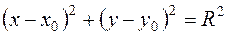
| ||
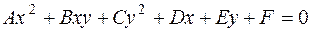
| ||
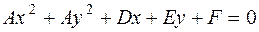
| ||
| IV. Практикум по матрицам и определителям | ||
Даны матрицы:
А = 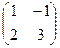 , В = , В =  , С = , С = 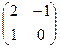 ,
Тогда матрица D = AB + 2C ,
Тогда матрица D = AB + 2C
| 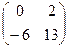
| |

| ||

| ||

| ||
Обратная матрица А-1 для матрицы
А =  имеет вид: имеет вид:
| 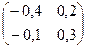
| |

| ||
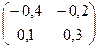
| ||
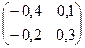
| ||
Ранг матрицы
А = 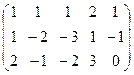 равен: равен:
| ||
Матрица С = АВ,
если А = (1 2 3), В =  , равна , равна
| (– 6) | |
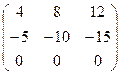
| ||
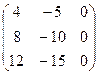
| ||

| ||
| V. Практикум по системам уравнений и аналитической геометрии | ||
Решая систему линейных уравнений
 методом Гаусса, система приводится к равносильной системе:
методом Гаусса, система приводится к равносильной системе:
| 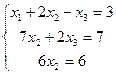
| |

| ||
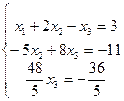
| ||

| ||
Решая систему линейных уравнений
 .
методом Гаусса, система приводится к равносильной системе: .
методом Гаусса, система приводится к равносильной системе:
| 
| |
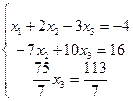
| ||
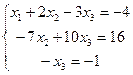
| ||
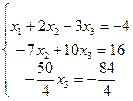
| ||
| Центр данной окружности х2+ у2 – 6х – 8у + 21= 0 находится в точке: | (3; 4) | |
| (-3; -4) | ||
| (-6; 8) | ||
| (6; -8) | ||
| Общее уравнение прямой, проходящей через точки А(7; -3) и В(4; 5) имеет вид: | 8х + 3у – 47 = 0 | |
у = 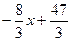
| ||
| 2х + 3у – 23 = 0 | ||
у = 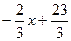
| ||
| Уравнение прямой с угловымкоэффициентом, проходящей через точку А(1; 2) параллельно прямой у = 7х – 3, имеет вид: | у = 7х – 5 | |
| у = 7х – 13 | ||
| х + 7у – 15 = 0 | ||
| 7х – у – 5 = 0 | ||
| Уравнение прямой с угловым коэффициентом, проходящей через точки А(2; 3) и В(-2; 2), имеет вид: | у = 
| |
| х = 2 | ||
у = 
| ||
| х – 4у + 10 = 0 | ||
| Уравнение прямой с угловым коэффициентом, проходящей через точки А(5; -3), В(4; 5), имеет вид: | у = - 8х – 37 | |
| у = - 8х – 43 | ||
| 8х + у + 37 = 0 | ||
| 8х + у + 43 = 0 | ||
| Кривая второго порядка, заданная уравнением 3х2 + у2 = 18, является | эллипсом с полуосями а =  , b=3 , b=3 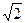
| |
гиперболой с действительной полуосью
а =  и мнимой полуосью b =3 и мнимой полуосью b =3 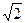
| ||
окружностью с центром в начале координат
и радиусом R = 3 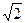
| ||
| эллипсом с полуосями а = 6, b = 18 | ||
Уравнение плоскости, проходящей через точку А(1; 0; -2) перпендикулярно вектору 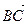 , где В(2; -1; 3), С(0; -3; 2), имеет вид: , где В(2; -1; 3), С(0; -3; 2), имеет вид:
| 2х +2у + z = 0 | |
| 2x + 2y + z + 4 = 0 | ||
| – 2x – z = 0 | ||
| – 2x – 2y – z + 4 = 0 | ||
Косинус угла между векторами 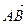 и и 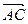 , где А(3; 3; -1), В(5; 5; -2),
С(4; 1; 1), равен , где А(3; 3; -1), В(5; 5; -2),
С(4; 1; 1), равен
| 
| |
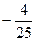
| ||
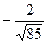
| ||
| Координаты точки пересечения прямых 5х + 6у + 8 = 0 и 3х + 5у + 5 = 0: | 
| |
| (0,2; -1,5) | ||
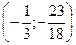
| ||
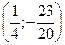
|
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 539; Нарушение авторских прав?; Мы поможем в написании вашей работы!