Свойства скалярного произведения

1. 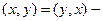коммутативность;

2. 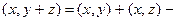дистрибутивность;

3. однородность;

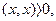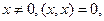4. если если

Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовымпространством.

Длиной (нормой) вектора 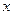в евклидовом пространстве называется корень квадратный из его скалярного квадрата: =

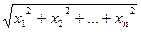
Свойства длины вектора:

1.

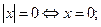
2. 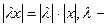действительное число;

3. (неравенство Коши-Буняковского);

4. 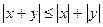-(неравенство треугольника).

Угол 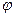между двумя векторам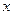и и 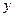определяется равенством:

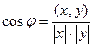, где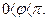

Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Если два ненулевых вектора ортогональны, то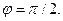

Векторы 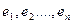n-мерного евклидова пространства образуют ортонормированный базис, если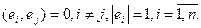

Теорема. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

Пример: система n единичных векторов 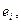у которых 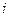-ая компонента равна единице, а остальные –нулю:

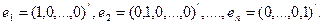
Линейные операторы

Рассмотрим два линейных пространства: 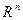размерност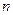и и размерности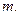

Если задан закон (правило), по которому каждому вектору 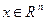ставится в соответствие единственный вектор то говорят, что задан оператор (преобразование, отображение) А (х), действующий из 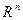в , и записывают у=А(х).

Оператор называется линейным, если для любых векторов 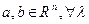выполняются соотношения:

1. 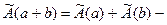свойство аддитивности;

2. 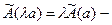свойство однородности оператора.

Вектор называется образом вектора х, а сам вектор х- прообразом вектора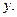

Если пространства 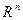и совпадают, то оператор А отображает пространство 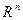в себя. Рассмотрим именно этот случай.

Выберем в 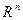базис 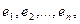запишем разложение произвольного вектора 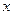по этому базису:

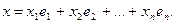
Применим к этому выражению линейный оператор 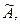в силу его линейности получаем:

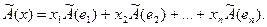
Поскольку 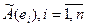-также вектор из 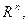то его можно разложить по базису :

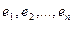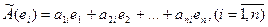
Тогда

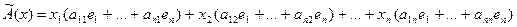
Перегруппируем сомножители в правой части, вынося за скобки базисные векторы 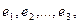получим:

(*)

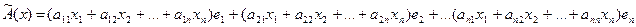С другой стороны, вектор имеющий в том же базисе 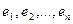координаты 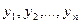можно записать так:

(**)

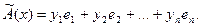Разложение вектора по базису единственно, следовательно, правые части (*) и (**) равны, поэтому:

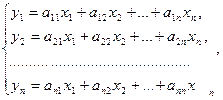
или в матричной форме:

Матрица каждый столбец которой состоит из координат образа 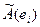соответствующего базисного вектора 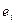в том же базисе 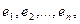называется матрицей оператора 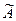в базисе 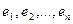, а ранг r матрицы А рангом оператора .

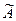Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Наоборот, всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.

Вектор х и его образ связаны матричным уравнением:

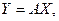
где А- матрица линейного оператора .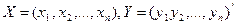

Пример: Линейный оператор 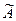в 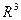в базисе 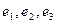задан матрицей 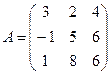Найти образ вектора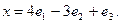

Решение: Применяем формулу перехода: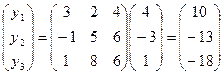

Образ вектора х имеет вид: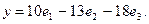

Суммой двух линейных операторов 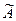и 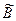называется оператор 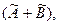определяемый равенством:

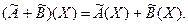
Произведением линейного оператора 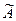на число 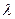называется оператор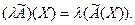

Произведением линейных операторов 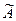и 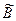называется оператор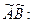

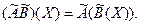
Все эти операторы удовлетворяют свойствам аддитивности и однородности, т.е. являются линейными.

Нулевой оператор 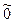переводит все векторы из 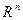в нулевые векторы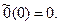

Тождественный оператор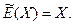

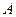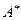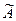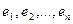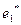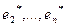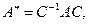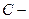Теорема. Матрицы и линейного оператора в базисах и , связаны соотношением: где матрица перехода от старого базиса к новому.

Пример. В базисе 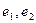оператор 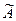имеет матрицу 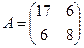. Найти матрицу оператора 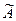в базисе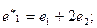

Решение, Матрица перехода здесь , а обратная к ней

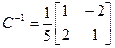
Следовательно,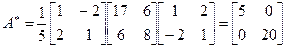

Собственные векторы и собственные значения линейного оператора

Вектор 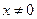называется собственным вектором линейного оператора 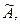если найдется такое число что

(*)

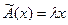Число 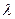называется собственным значением оператора 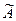(матрица А), соответствующим вектору 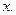Под действием линейного оператора 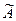собственный вектор переходит в вектор, коллинеарный самому себе.

Перепишем (*) в матричной форме: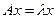

В развернутом виде:

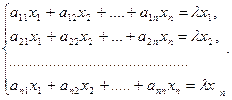
Представим в однородном виде:

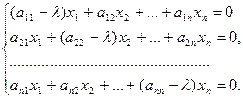
Эта система (однородная) всегда имеет нулевое (тривиальное) решение х=0. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы равнялся нулю:

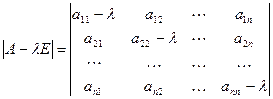= 0 (**)

Определитель является многочленом n-ой степени относительно 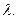Это – характеристический многочлен оператора 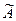или матрицы А, а уравнение (**) – характеристическое уравнение оператора 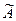или матрицы А.

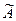Характеристический многочлен линейного оператора не зависит от выбора базиса, т.е. где матрицы оператора в старом и новом базисах соответственно.

Пример. Найти собственные значения и собственные векторы линейного оператора заданного матрицей

1 4

А = 9 1.

Решение. Составим характеристическое уравнение

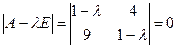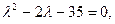, или откуда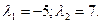

Находим собственный вектор 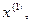отвечающий собственному значению

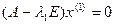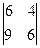
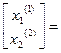
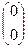или , откуда 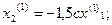Примем 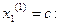отсюда векторы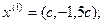 являются собственными векторами линейного оператора 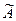с собственным значением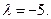

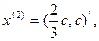
Аналогично для векторы являются собственными векторами линейного оператора 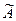с собственным значением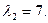

Наиболее простой вид принимает матрица А линейного оператора 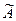, имеющего n линейно независимых собственных векторов 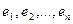с собственными значениями, соответственно равными Матрица оператора 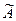в базисе, составленном из его собственных векторов, является диагональной и имеет вид:

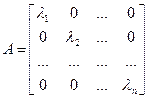
Верно и обратное: если матрица А линейного оператора 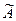в некотором базисе является диагональной, то все векторы этого базиса – собственные векторы оператора

Кроме того, если линейный оператор имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.

Линейная модель обмена (модель международной торговли)

Пусть n стран 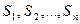имеют национальный доход 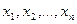соответственно, 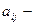доля национального дохода, которую j-ая страна тратит на покупку товаров у I-ой страны. Считаем, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.

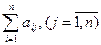(1)

Матрица 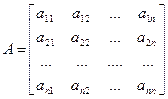называется структурной матрицей торговли.

Дата добавления: 2014-11-26