Размерность и базис векторного пространства

Линейные операторы. Собственные значения линейного оператора

Евклидово пространство

Векторы и операции над ними.

Векторная алгебра

Лекция № 8 - 9

Привести примеры определенной и неопределенной СЛАУ.

3. Какие основные методы решения СЛАУ?

План лекции:

Векторы и операции над ними

Вектор – направленный отрезок 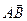с начальной точкой А и конечной точкой В.

B

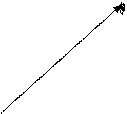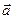
A

Его можно обозначить по разному: 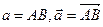, 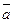= АВ.

Длина (модуль) вектора 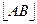- это число, равное длине отрезка АВ.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Нулевой вектор (нуль-вектор)- это вектор, у которого начало и конец совпадают. Его длина равна нулю, направление произвольно, и он считается коллинеарным любому вектору.

Произведение вектора 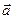на число 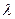-это вектор длиной 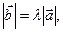, направление которого совпадает с 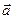, если 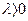, и противоположно ему, если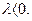

Противоположный вектор 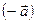-это произведение 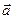на (-1).

Сумма двух векторов 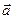и определяется по правилу треугольника:

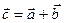
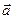
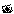
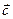
Сумма нескольких векторов – результат последовательного применения правила треугольника, т.е. правило многоугольника.

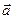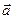Разность векторов и - это сумма вектора и вектора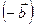

В параллелограмме, построенном на векторах 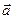и , одна диагональ представляет сумму 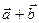, а другая – разность .

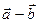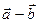
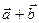
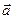
Перенесем вектор 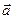параллельно самому себе так, чтобы его начало совпало с началом координат. Тогда координатами вектора 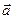называются координаты его конечной точки. Тогда вектор можно записать в координатной форме:

- на плоскости

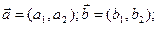
- в пространстве

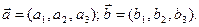
Можно показать, что

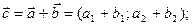
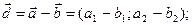
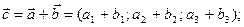и т.д.

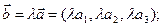
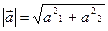или

.

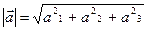Скалярное произведение (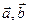) двух векторов 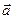и - это число, равное произведению длин этих векторов на косинус угла между ними:

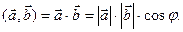
В координатной форме

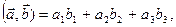
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Если 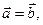то 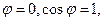и получаем скалярный квадрат вектора:

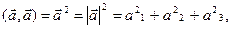
который равен квадрату его длины.

Расстояние между двумя точками плоскости А(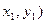 и В (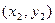 можно рассматривать как длину вектора =

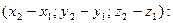
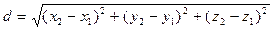
Угол между векторами 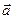и определяется по формуле:

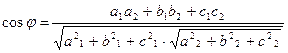
n-мерное векторное пространство

n-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде где 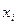- I-ая компонента вектора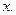

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е.

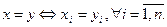
Сумма двух векторов:

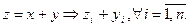
Произведение вектора на действительное число :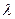

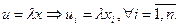
Свойства операций над векторами:

1. x+y= y+x;

2. (x+y)+z=x+(y+z);

3.

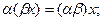
4.

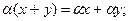
5.

6. Существует нулевой вектор 0=(0,…,0) такой, что х+0=х,

7. Для любого х существует (-х) такой, что х+(-х)=0;

8.

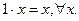
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющих приведенным выше свойствам, называются векторным пространством.

Пример: множество алгебраических многочленов степени не выше n

Размерность и базис векторного пространства

Вектор 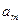называется линейной комбинацией векторов векторного пространства R, если он равен следующей сумме:

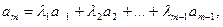где 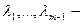произвольные действительные числа.

Векторы 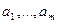векторного пространства R называются линейно зависимыми, если существуют такие числа 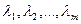, не равные одновременно нулю, что их линейная комбинация равна нулевому вектору:

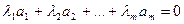
В противном случае (т.е. когда нуль-вектор получается только при 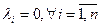) векторы называются линейно независимыми.

Линейное пространство R называется n-мерным, если в нем существует n линейно независимых векторов, а любые (n+1) векторов уже являются линейно зависимыми. Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Обозначается размерность dim ®.

Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.

Теорема. Каждый вектор можно представить и притом единственным образом в виде линейной комбинации векторов базиса.

Такая линейная комбинация

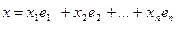
называется разложением вектора х по базису 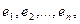а числа 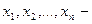координатами вектора х относительно этого базиса.

Теорема. Если система линейно независимых векторов пространства R и любой вектор а в нем линейно выражается через 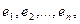то пространство R является n-мерным, а векторы его базисом.

Переход к новому базису

Пусть в пространстве R имеются 2 базиса:

Старый 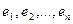и новый 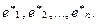Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

…………………… ()

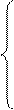
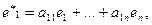
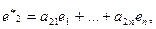
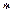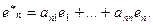
Эта система означает, что переход от старого базиса к новому задается матрицей перехода 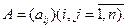Эта матрица неособенная (т.е. невырожденная), т.к. в противном случае ее строки (а значит, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса к старому осуществляется с помощью обратной матрицы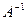

Найдем зависимость между координатами вектора в разных базисах.

Пусть х имеет координаты:

Подставим значения 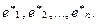из системы (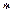) в левую часть последнего равенства, получим:

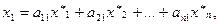
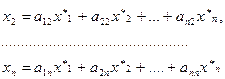
или в матричной форме:

Евклидово пространство

Скалярным произведением двух векторов 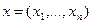и 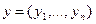называется число: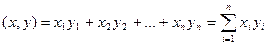

Экономический смысл скалярного произведения: если вектор объемов различных товаров, а 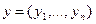- вектор их цен, то ()- суммарная стоимость этих товаров.

Дата добавления: 2014-11-26