Базы знаний и их применение для формирования экономических решений

Базы знаний — это знания человека, представленные в памяти компьютера в соответствии с какой-либо моделью. Наиболее рас­пространенными моделями в настоящее время являются: деревья выводов (правила, продукции), деревья целей и семантические сети.

Дерево вывода. Дерево вывода — это множество объединенных правил, отражающих условия выполнения некоторого процесса. Правила представляют собой языковую конструкцию вида

ЕСЛИ <условие, ct(условия)>, ТО <заключение, ct(заключения)> сt(правила),

где ct (условия), ct (заключения), ct (правила) соответственно коэф­фициенты определенности условия, заключения и правила.

Значение ct, равное 0, указывает на полную неопределенность, а 1 — на полную определенность. В дереве указывают значения в этом диапазоне.

Множество правил объединяются в дерево вывода.

Рассмотрим, как знания такого рода представляются графичес­ки, а также как рассчитывается коэффициент определенности выводов. Правило с одним условием вида ЕСЛИ А, ТО В графи­чески представляется следующим образом:

ct (В) = 0,08

О

ct (правила) = 0,2

О

ct (А) =0,4

Здесь А — это условие, В — заключение. Далее условимся заклю­чение, получаемое с помощью правила, изображать сверху, а условия снизу. Число рядом с условием указывает на его определенность, а число рядом с линией — на определенность самого правила.

В правиле может быть несколько условий, связанных между собой союзами И или ИЛИ.

Сплошная или пунктирная дуга указывает на вид объединения условий: со­юзом И или союзом ИЛИ соответственно. Число, указанное ря­дом с дугой (сплошной или пунктирной), указывает на определен­ность правила, а числа рядом с условиями — на определенность условий. Лицо, принимающее решение, присваивает условиям (А, В, С) и правилу некоторый коэффициент определенности от 0 до 1.

Например,

ЕСЛИ А и В и С, ТО Е; ЕСЛИ А или В или С, ТО Е.

С помощью специальных формул рассчитывается коэффици­ент определенности для заключения. Для простого правила, со­держащего лишь одно условие, например ЕСЛИ Е, ТО С, коэф­фициент определенности для заключения С рассчитывается так:

ct (С) = ct (Е) • ct (правила),

где ct (С), ct (Е) и ct (правила) — коэффициенты определенности соответственно заключения С, условия Е и правила.

Например, при ct (Е) = 0,4; ct (правила) = 0,2 коэффициент определенности заключения равен ct (С) = 0,08.

Если в правиле несколько условий, связанных союзом И, то для расчета коэффициента определенности заключения применя­ется следующая операция:

ЕСЛИ(Е1 и Е2), ТО С.

ct (С) = min(ct (Е1), ct (Е2)) • ct (правила).

Для правила, в котором присутствует несколько условий, свя­занных связкой ИЛИ, применяется операция вида:

ЕСЛИ(Е1 или Е2), ТО С.

ct(С) = max(ct(Е1), ct(Е2)) • ct(правила).

Например, ЕСЛИ (Е1 и Е2),ТО С. При ct (Е1) = 0,7; ct (Е2) = 0,6; ct (правила) = 0,8; ct (условия) = min(0,7; 0,6) = 0,6 ко­эффициент определенности заключения равен ct (С) = 0,6 • 0,8 = 0,48.

Для заключения А, вывод которого представлен на рис. 3.21, при ct (Д) = 0,8; ct (Е) = 0,5; ct (О) = 0,6; ct (пр1) = 0,7; ct (С) = 0,4; ct (пр2) = 0,3 его коэффициент определенности А равен ct (А) = 0,12.

Дерево целей. Представление знаний в виде дерева целей воз­можно, если известны цель управления и формулы, по которым можно рассчитать уровень достижения каждой подцели. Допус­тим, целью является увеличение прибыли, которая может быть достигнута за счет увеличения выручки и снижения затрат, что можно представить графически (см. рис. 42).

На рис. 42 с помощью знаков «+» и «-» показаны желаемые направления изменения подцелей: В— выручка: увеличение; 3— затраты: снижение; П— прибыль: увеличение. Если В= 20, 3=15, то по формуле В = П— 3 получим

П= 5.

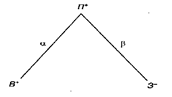
Рис. 42. Графическая иллюстрация достижения цели «Увеличить прибыль»

Используется дерево целей следующим образом: допустим, необходимо поднять прибыль до 7 ед. Для этого нужно устано­вить приоритеты в достижении данной цели, чему служат коэффициенты аир. Сумма этих коэффициентов всегда равна 1. Пользуясь типовыми формулами обратных вычислений, можно определить, какими должны быть выручка и затраты:

где ∆В и ∆З — соответственно искомый прирост выручки и иско­мое снижение затрат.

Подставив исходные данные, получим:

κ₁=1,07; κ₂=1,04; В+ΔВ= 21,4; З-ΔЗ= 14,4.

Сделаем проверку правильности полученных результатов:

П+△П=21,4- 14,4 = 7.

Дерево целей можно продолжить, если указать, из чего состо­ят выручка и затраты. Это позволит рассчитать управляющие воз­действия более детального характера.

Семантическая сеть. Это ориентированный граф, в узлах ко­торого находятся имена объектов, а стрелки указывают на отно­шения между ними (рис. 3.24). Из неизмеримого множества от­ношений часто используются часть-целое, свойства и функцио­нальные связи (производит, находится и т.д.).

Семантическая сеть обрабатывается на основе принципа сопо­ставления объекта и отношения, указанных в запросе, с объекта­ми и отношениями, имеющимися в семантической сети. Напри­мер, если запрос имеет вид: «Что производит ОАО "Горизонт?"», будет выделен тот фрагмент сети, где фигурируют указанный объект («Горизонт») и отношение «производит». Ответом будет: «ОАО "Горизонт" производит кинескопы».

С помощью приведенной на рис. 43 семантической сети мож­но получить ответы на следующие вопросы:

1. Какие предприятия производят кинескопы?

2. В каком регионе находится город Тула?

3. Кто является поставщиком кинескопов?

4. Какие кинескопы производит ОАО «Горизонт»?

Рисунок 43. Семантическая сеть

Дата добавления: 2014-11-26