Концептуальная модель принятия решения

Ведем обозначения и определения, на которых основаны следующие аксиомы:

Аксиома 1. Существование относительных предпочтений. Для любой (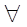) пары исходов х₁ и х₂ справедливы утверждения х₁ = х₂, х₁, > х₂ или х₂ > х₁

Аксиома 2. Транзитивность.

Аксиомы 1 и 2 вместе означают, что ЛПР может провести ранжировку относительно предпочтения различных возможных исходов. Эти аксиомы не утверждают, что лицо, принимающее решение, может объяснить свои предпочтения.

Аксиома 3. Сравнение БСИ.

Аксиома 4. Численная оценка предпочтений. Каждому возможному исходу х ЛПР может поставить в соответствие число π (х), (где 0 < π (х) < 1), такое, что

Х = И(х*, π (х), х₀).

Аксиомы 3 и 4 определяют для ЛПР меру относительного предпочтения различных исходов π(х), называемую вероятностью равноценности или субъективной вероятностью.

Эта вероятность отражает степень уверенности ЛПР в том, что событие Ф наступит, и в ее основе лежит готовность данного ЛПР действовать в соответствии с этой уверенностью.

Субъективная вероятность, основанная на физических явлениях. В некоторых ситуациях можно предположить, что все возможные исходы некоторого эксперимента (случайного события) имеют равные шансы на появление в результате эксперимента; Эта означает, что если существует К возможных исходов, то субъективная вероятность каждого из них равна 1/К.

Субъективная вероятность, основанная на имеющихся данных. Если имеются данные о возможности наступления событий, интересующих ЛПР, то их можно использовать для формирования суждений о вероятностях событий. Если в каждом из испытаний наблюдалось одно из взаимоисключающих событий, причем Кн раз наблюдалось интересующее нас событие, то вероятность его принимается равной частоте события, т.е. Кн/К.

Субъективная вероятность, основанная на результатах моделирования. Вероятности стохастических событий часто невозможно получить на основе статистических данных из-за их отсутствия или недостатка. Теория исследования операций рекомендует в этом случае построить аналитическую или имитационную модель явления,

Аксиома 5. Численная оценка неопределенности суждений Каждому возможному событию Ф, которое может влиять на исход решения, можно поставить в соответствие число Р(Ф) из интервала [0, 1] такое, что становятся равноценными БСИ И (х*, Р(Ф), х₀) и ситуация, при которой ЛПР получает х*, если происходит событие Ф, и х₀, если событие Ф не происходит. Значение Р(Ф) определяет ЛПР.

Аксиома 6. Равноценность задач. Если модифицировать задачу принятия решения путем замены одного исхода другим, которые равноценны для ЛПР, то обе задачи принятия решения (старая и модифицированная) будут равноценны для этого ЛПР.

Аксиома 7. Эквивалентность условного и безусловного предпочтений. Пусть И1 и И2 – два БСИ, возможные только при наступлении события Ф. Если известно, наступит событие Ф или нет, то ЛПР должно иметь те же предпочтения между И1 и И2, как и при отсутствии этой информации.

Если ЛПР опирается на данные аксиомы, то ему надлежит всегда выбирать альтернативы так, чтобы максимизировать ожидаемую полезность.

Для описания формальной модели принятия решения ЛПР введем следующие обозначения:

П – полезность – есть функция альтернативы (возможного решения):

П = Ф(А),

где Ф – механизм перебора и выбора альтернатив;

А – альтернатива – совокупность (стратегии, результата и риска):

А = [(С, Н, В), (Д, R)] (22),

где (С, Н, В) – способ достижения результата – стратегий;

С = (состояние, цель, план, исходы) (23),

где состояние – исходная информация и представления ЛПР о тeкущей ситуации,

цель – представления ЛПР о желаемой ситуации

план – совокупность возможных последовательностей действий, i идущих к достижению цели,

исходы – возможные последствия реализаций плана, среди которых по крайней мере один опасен;

Н = (субъективные вероятности исходов = представления ЛПР и неопределенности);

В = (возможности, среди которых, по крайней мере, одна нежелательна = последствия исходов, среди которых, по крайней мере, один опасен).

Д – результат (желаемые возможности решения);

R – риск (нежелательные возможности решения);

МП* – максимальная ожидаемая полезность, т.е.

МП* = max П k = max F (МДk,MRk) (24)

(k) (k)

где Пк = F (МДк, MRk) – ожидаемая ЛПР полезность k-й альтернативы;

k – индекс альтернативы (k = 1,..., К);

МДk – ожидаемый ЛПР результат выбора k-й альтернативы;

MRk – ожидаемый ЛПР риск выбора k-й альтернативы;

В соответствии с аксиомами теории принятия решений ЛПР должно всегда выбирать альтернативу k* с максимальной ожидаемой полезностью, т.е.

Пk* = F (МД k *, MRk*) = МП* (25).

Следует отметить, что специфической чертой решений, принимаемых бизнесменами, является характерная зависимость результат от риска: чем больше ожидаемый результат, тем выше риск. Это означает, что максимизировать полезность решения можно или путем максимизации ожидаемого результата при фиксированном уровне риска, или путем минимизации риска при фиксированном уровне ожидаемого результата.

Выбор того или иного варианта постановки предопределяется предпочтениями ЛПР. Формальная запись функций выбора решений имеет вид (26):

Пk* = max МД k (26)

(k)

при условии (для всех k) MRk < R₀,

где R₀, – допустимый для субъекта уровень риска,

«Кто не рискует, то не пьет шампанского»

П k * = min MRk (27),

( k )

при условии (для всех k) МДк > Д₀,

где Д₀, – приемлемый для субъекта уровень результата (например, дохода).

«Лучше синица в руках, чем журавль в небе»

Предполагается, что существует единственная мера эффективности X, относительно которой необходимо оцени предпочтения лица, принимающего решение. Нужно оценить полезность π (х) каждого возможного исхода x_v x₂,... Поскольку число возможных исходов обычно велико, необходимо (и проще) оценить функцию полезности π (х).

Процедура оценки функций полезности включает пять этапов: предварительный анализ для фактической оценки; определение качественных параметров; 3) формирование количественных ограничений; выбор функции полезности; проверка на согласованность.

Дата добавления: 2014-11-26