Штучна нейронна мережа

Найбільш містке визначення ШНМ таке:

Штучна нейронна мережа – це суттєво паралельно розподілений процесор, здатний зберігати і відтворювати дослідне знання.

Вона схожа з мозком людини у двох аспектах:

– мережа набуває знань у процесі навчання;

– для збереження знань мережа використовує сили міжнейронних з’єднань (синаптичних ваг).

	w 0 w 1
	w 2 w n
		Σ

x ₁

x ₂

S

h

y

...

x _n

Рис. 3.2. Схема штучного нейрона

Штучний нейрон, схему якого показано на рис. 3.2, працює так.

Сигнали x_i (i =1,..., n), що надходять на вхід нейрона, множаться на

вагові коефіцієнти w_i (синаптичні ваги). Далі вони додаються і вислі-

дний сигнал зсувається на величину w ₀ порогового зсуву:

S = x_i + w ₀. (3.1)

Потім вихідний сигнал S подається на вхід блоку, що реалізує

нелінійну активаційну функцію нейрона h (S).

3.4. Типи активаційних функцій

Традиційно активаційні функції східчасті, тобто сигнал на виході

нейрона з’являється тільки тоді, коли сумарний вхідний вплив пере-

вищує певне порогове значення.

Одна з умов реалізації якогось перетворення за допомогою ШНМ –

це нелінійність її активаційної функції. Для перетворень найчастіше

використовують такі функції: лінійні, лінійні з насиченням (рис. 3.3,

а, б); порогові функції (рис. 3.3, в, г); сигмоподібні тангенціальні фун-

кції (рис. 3.3, д); сигмоподібні логарифмічні (рис. 3.3, е); гармонічні

функції та радіально-базисні.

Хоча лінійна функція у чистому вигляді й не дозволяє реалізува-

ти будь-якого перетворення, проте вона часто може виявитись корис-

ною для простого масштабування вихідного сигналу нейрона.

	h S б h S г h S е

h

S

а

h

S

в

h

S

д

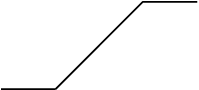
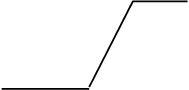
Рис. 3.3. Графіки активаційних функцій: а – лінійної з насиченням;

б – лінійної з насиченням (зміщеної); в – порогової; г – порогової (зміщеної);

д – сигмоподібної тангенціальної; е – сигмоподібної логарифмічної

Сигмоподібні функції найчастіше застосовують у нейронних ме-

режах. Їх описують такими функціональними залежностями:

h (S) = -1 – тангенціальною;

1+ e ^{- x}

h (S) = – логарифмічною.

1+ e ^{- x}

Функції синуса або косинуса (гармонічні функції) досить часто

використовують у нейронних мережах для подання періодичних пе-

ретворень.

Радіально-базисна функція має такий вигляд: h (S) = e ^{- x 2}.

Наведені активаційні функції найбільш вживані, але в жодному

разі не перекривають усіх можливих.

Дата добавления: 2014-11-16