Метод зворотного поширення похибки

(Error Back Propagation)

Метод зворотного поширення похибки вперше був сформульований

Вербосом 1974 року. Але визнаний він був значно пізніше, 1986 року,

коли його «перевідкрив» Румельхарт, Хінтон і Вільямс. За своєю суттю –

це метод градієнтного спуску, котрий застосовують для настроювання

вагових коефіцієнтів так, щоб мінімізувати функцію похибки (4.1).

Мінімізація за методом градієнтного спуску означає підстрою-

вання вагових коефіцієнтів

∂ E ∂ w_ij

, (4.2)

(

∆ w_ij^{n )} = -з

де w_ij – ваговий коефіцієнт синаптичного зв’язку, що з’єднує i -й ней-

рон шару n –1 з j -м нейроном шару n, η – коефіцієнт швидкості нав-

чання, 0< η <1. Користуючись правилами диференціального числен-

ня, можна записати:

	∂ E ∂ wij		∂ E

= = = ∂ y      

∂ w_ij

, (4.3)

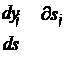де y_j – вихід j-го нейрона, а s_j – зважена сума його вхідних сигналів, тобто аргумент його нелінійної активаційної функції:

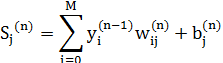
Оскільки множник dy _j ds _j є похідною цієї функції за її аргументом, то з цього випливає, що похідна активаційної функції повинна бути визначеною на всій осі абсцис. У зв’язку з цим активаційні функції з розривами першого і другого родів не підходять для нейронних мереж, що навчаються методом зворотного поширення похибки.

Наприклад, у випадку гіперболічного тангенса маємо:

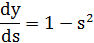
Третій множник 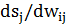дорівнює виходу i-го нейрона з попереднього шару, 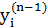. Щодо першого множника в (4.3), то його легко розкласти так:

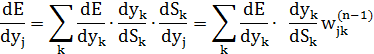
Тут додавання за k виконують серед нейронів шару n+1. Вводячи нову змінну

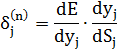
Отримуємо рекурсивну формулу для розрахунків величини 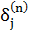шару n за величинами 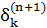наступного шару n+1:

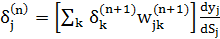(4.4)

Для останнього ж, вихідного шару маємо:

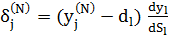(4.5)

Тепер ми можемо записати (4.2) в розгорнутому вигляді:

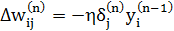(4.6)

Інколи для надання процесу корекції ваг деякої інерційності, що згладжує різкі стрибки під час переміщення поверхнею цільової функції, вираз (4.6) доповнюється значенням зміни ваги на попередній ітерації:

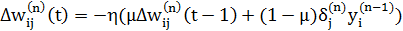, (4.7)

де 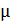- коефіцієнт інерційності, t- номер поточної ітерації.

Отже, повний алгоритм навчання ШНМ за допомогою процедури зворотного поширення похибки має такий вигляд:

Крок 1. Ініціалізація ваги і зміщення, які задають випадково.

Наприклад, в діапазоні від –1 до 1.

Крок 2. Розрахування виходу мережі і похибки за вектором входу і відповідним йому вектором бажаного виходу із еталонних даних.

Крок 3. Розрахування δ^{( N )} для вихідного шару за формулою (4.5).

Крок 4. Розрахування зміни ваг ∆w^{( N )} для вихідного шару за формулою (4.6) або (4.7).

Крок 5. Розрахування за формулами (4.4) і (4.6), або (4.4) і (4.7) відповідно δ^{( n)} і ∆w^{( n)} для всіх інших шарів.

Крок 6. Коригування всіх ваг у ШНМ:

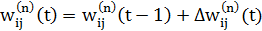(4.8)

Крок 7. Перехід на крок 2, якщо похибка мережі суттєва, а якщо ні – то закінчення навчання.

4.4. Навчання нейронних мереж за допомогою генетичних алгоритмів

Оскільки навчання ШНМ – це пошук такого стану параметрів мережі (синаптичних ваг і порогових зміщень), який мінімізує функцію похибки, котру можна задати у вигляді (4.1). Одним із найбільш ефективних методів глобальної оптимізації є генетичні алгоритми (ГА). Під час використання ГА для навчання ШНМ параметрами оптимізації є синаптичні ваги і порогові зміщення. Функція пристосованості буде обернено пропорційною до функції похибки (4.1).

Дата добавления: 2014-11-16