Гранные поверхности

Классификация поверхностей

Лекция 2. Решение метрических задач

2.1 Графическое определение простых поверхностей.

2.2 Метод вспомогательных секущих плоскостей.

2.3 Пересечение конической поверхности с прямой.

2.4 Пересечение гранной и кривой поверхностей.

2.5 Пересечение двух кривых поверхностей.

2.6 Метод вспомогательных секущих сфер. Пересечение поверхностей вращения.

В архитектурно-строительной практике широко применяются пространственные криволинейные формы, основу которых представляют различные кривые поверхности в их "чистом" геометрическом виде или составленные из нескольких поверхностей. При выборе исходной поверхности архитектор должен в совершенстве знать геометрию этих поверхностей: их основные характеристики, свойства, принципы образования и изображения и др.

Классификация поверхностей на протяжении длительного периода была предметом научных исследований, но пока не удалось установить единую систему, так как за ее основу могут быть взяты разные критерии: характер образующей, признак развертывания и прочее.

В данной лекции приводится один из примеров классификации.

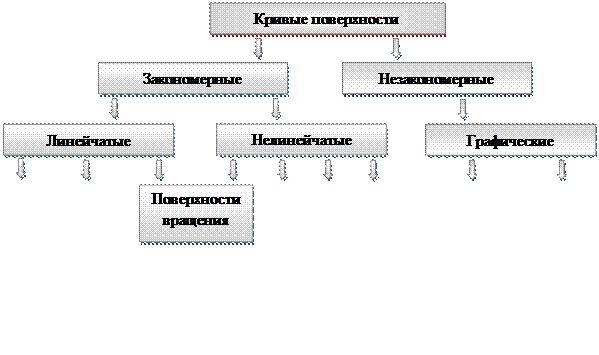Геометрические тела, ограниченные плоскими многоугольниками (гранями), называются гранными (призма, пирамида). Рассмотрим изображение гранных поверхностей и нахождение точек, лежащих на поверхностях этих тел.

На рисунке 2.1 изображена прямая правильная шестигранная призма. Если точка лежит на ребре (например, точка 1), которое является горизонтально проецирующим, то горизонтальная проекция этой точки 1₁ совпадает с горизонтальной проекцией ребра А₁. При построении горизонтальных проекций точек, лежащих на боковой поверхности грани призмы, например, точки 2 и 3, достаточно провести линии связи из фронтальных проекций точек (2₂ и 3₂), на контур горизонтальной проекции призмы, см. рисунок 2.1.

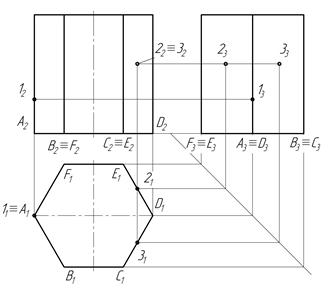
Рисунок 2.1

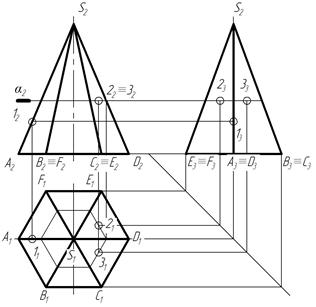
Рисунок 2.2

Дата добавления: 2014-11-16