Конические сечения

Пересечение кривых поверхностей плоскостью

Теорема Монжа (самост)

Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения. В этом случае для построения линии пересечения поверхностей используется теорема Г.Монжа, которая формулируется так:

Если две поверхности вращения второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечении линий касания.

В соответствии с этой теоремой линии пересечения конуса и цилиндра описанного около сферы (рисунок 6.7) будут плоскими кривыми – эллипсами, фронтальные проекции которых изображаются прямыми 1₂4₂ и 2₂3₂, проходящими через 5₂5₂' – точки линий пересечения окружностей касания.

В зависимости от положения секущей плоскости, различают следующие виды конических сечений (рисунок 2.4):

I – окружность – секущая плоскость перпендикулярна оси.

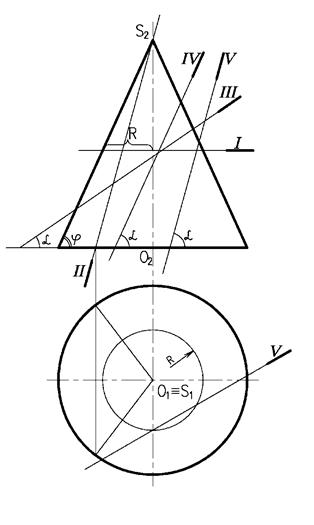II – треугольник – секущая плоскость проходит через вершину конуса.

III – эллипс – секущая плоскость пересекает все образующие конуса (α < φ).

IV – парабола – секущая плоскость параллельна образующей конуса (α = φ).

V – гипербола – секущая плоскость параллельна двум образующим конуса (α > φ).

Построение линии сечения конуса по окружности и треугольнику не вызывает затруднений. Для окружности – замеряем радиус, для треугольника – находим точки пересечения с основанием. Построения показаны на рисунок 5. 2.

Для построения сечений конуса по эллипсу, параболе, гиперболе, необходимо определить несколько точек, принадлежащих линии сечения. Для нахождения этих точек используется метод плоскостей посредников.

Алгоритм решения задачи состоит в следующем:

а) проводят плоскости посредники;

б) строят линии пересечения посредников с данной поверхностью и с плоскостью;

в) определяют точки пересечения между собой полученных линий;

г) соединяют полученные точки с учетом видимости.

Для примера рассмотрим построение конуса по эллипсу (рисунок 5.3). Т.к. плоскость Ϭ фронтально-проецирующая, необходимо построить горизонтальную проекцию сечения. В первую очередь строятся опорные точки сечения, в данном случае высшая и низшая точка сечения, лежащая на контурных образующих (1 и 2). 1,2 – большая ось эллипса. Чтобы сечение получилось правильным, необходимо найти положение малой оси 3,4. Для нахождения горизонтальной проекции 3₁, 4₁, через фронтальные проекции точек проводим вспомогательную горизонтальную плоскость посредник, которая рассекает конус по окружности. Таким же образом строим промежуточные точки 5,6,7,8. Полученные точки соединяем плавной кривой линией.

Аналогично строятся линии пересечения других поверхностей плоскостями. Гораздо проще строить сечения поверхностей, проецирующими плоскостями, поэтому, если задана плоскость общего положения, имеет смысл выполнить замену плоскостей проекций, перпендикулярно заданной плоскости, а затем уже строить сечение.

Дата добавления: 2014-11-16